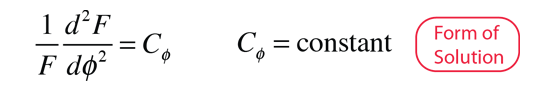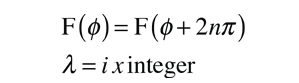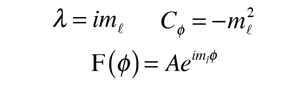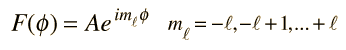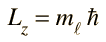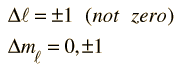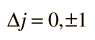Selection Rules for Electronic Transitions
In spectral phenomena such as the Zeeman effect it becomes evident that transitions are not observed between all pairs of energy levels. Some transitions are "forbidden" ( i.e., highly improbable) while others are "allowed" by a set of selection rules. The number of split components observed in the Zeeman effect is consistent with the selection rules:
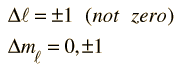
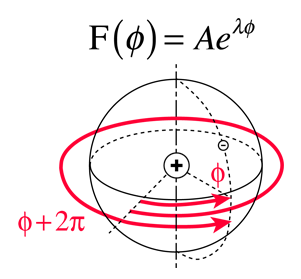
These are the selection rules for an electric dipole transition. One can say that the oscillating electric field associated with the transitions resembles an oscillating electric dipole. When this is expressed in quantum terms, photon emission is always accompanied by a change of 1 in the orbital angular momentum quantum number. The magnetic quantum number can change by zero or one unit.
Another approach to the selection rules is to note that any electron transition which involves the emission of a photon must involve a change of 1 in the angular momentum. The photon is said to have an intrinsic angular momentum or "spin" of one, so that conservation of angular momentum in photon emission requires a change of 1 in the atom's angular momentum. The electron spin quantum number does not change in such transitions, so an additional selection rule is:

The total angular momentum may change by either zero or one:
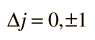 An exception to this last selection rule is that you cannot have a transition from j=0 to j=0; i.e., since the vector angular momentum must change by one unit in an electronic transition, j=0 -> 0 can't happen because there is no total angular momentum to re-orient to get a change of 1.
An exception to this last selection rule is that you cannot have a transition from j=0 to j=0; i.e., since the vector angular momentum must change by one unit in an electronic transition, j=0 -> 0 can't happen because there is no total angular momentum to re-orient to get a change of 1.
|