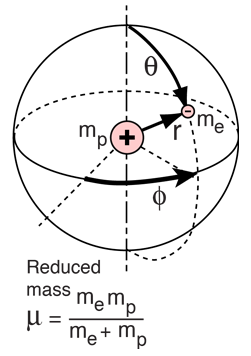
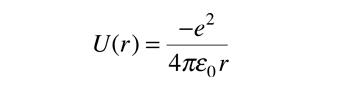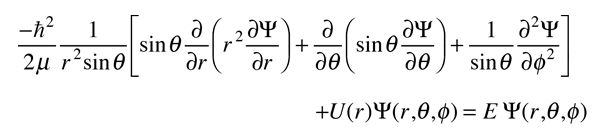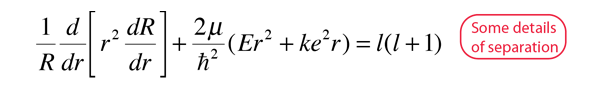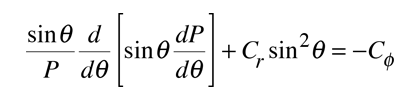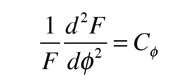The Hydrogen Atom
|
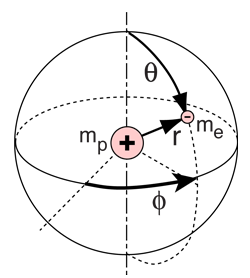
The solution of the Schrodinger equation for the hydrogen atom is a formidable mathematical problem, but is of such fundamental importance that it will be treated in outline here. The solution is managed by separating the variables so that the wavefunction is represented by the product:  The separation leads to three equations for the three spatial variables, and their solutions give rise to three quantum numbers associated with the hydrogen energy levels. |
Schrodinger equation concepts
Hydrogen concepts
| HyperPhysics***** Quantum Physics | R Nave |