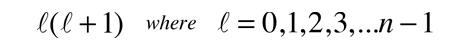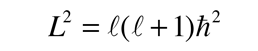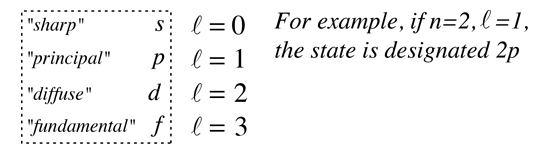The Colatitude Equation
Upon separation of the Schrodinger equation for the hydrogen atom, the colatitude equation is:
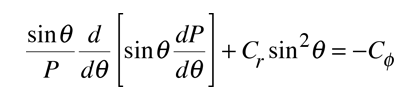
The solution of the azimuthal equation provides the constraint
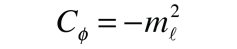
A detailed solution involves conversion of the above equation to a form in which the variable is cos θ . It can be solved by a series expansion (polynomial) method in which the conditions for a solution force the remaining constant to be of the form
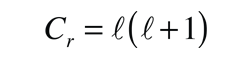
producing the orbital quantum number. The solutions to the colatitude equation are in a form called associated Legendre functions, and when properly normalized form part of the hydrogen wavefunctions.
Schrodinger equation concepts
Hydrogen concepts
| HyperPhysics***** Quantum Physics | R Nave |