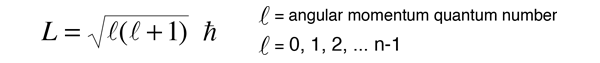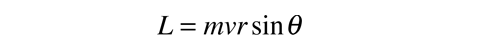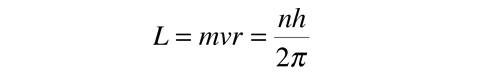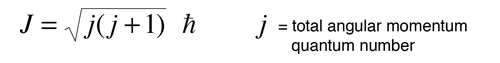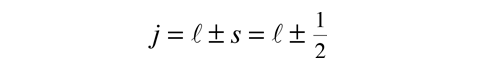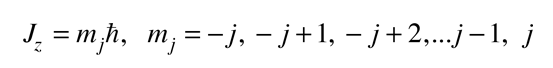Quantized Angular Momentum
In the process of solving the Schrodinger equation for the hydrogen atom, it is found that the orbital angular momentum is quantized according to the relationship:
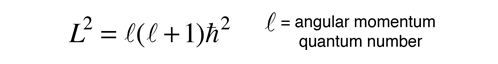
It is a characteristic of angular momenta in quantum mechanics that the magnitude of the angular momentum in terms of the orbital quantum number is of the form
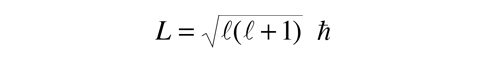
and that the z-component of the angular momentum in terms of the magnetic quantum number takes the form
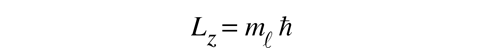
This general form applies to orbital angular momentum, spin angular momentum, and the total angular momentum for an atomic system. The relationship between the magnitude of the angular momentum and its projection along any direction is space is often visualized in terms of a vector model.
| HyperPhysics***** Quantum Physics | R Nave |