Energy Calculation for Rigid Rotor Molecules
In many cases the molecular rotation spectra of molecules can be described successfully with the assumption that they rotate as rigid rotors. In these cases the energies can be modeled in a manner parallel to the classical description of the rotational kinetic energy of a rigid object. From these descriptions, structural information can be obtained (bond lengths and angles). The most straightforward examples are those of diatomic molecules.
Energy calculations in quantum mechanics involve the solution of the Schrodinger equation with a properly formulated Hamiltonian to represent the energy operator. The form of the Hamiltonian can often be implied from the nature of the classical energy of such a physical system. The process involves finding the quantum mechanical operators associated with the constituents of the system energy. The energy of a freely rotating rigid rotor is simply the rotational kinetic energy, which can be expressed in terms of the angular momentum. The general form of operators associated with momenta are:

Since the rotational kinetic energy of the rigid rotor can be expressed in terms of the angular momentum, we can imply the form for the Hamiltonian associated with the rotation around a single principal axis.

For this limited case of rotation about a single axis, the Schrodinger equation can be formulated in terms of the total angular momentum and the form of the energy eigenvalues implied.
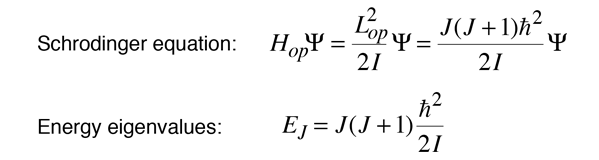
To treat the more general three-dimensional rotation of a rigid molecule, it is necessary to formulate the Hamiltonian in three dimensions. It is appropriate to formulate it in spherical polar coordinates, and this adds significantly to the mathematical complexity. The square of the angular momentum operator takes the form of a Laplacian and the Schrodinger equation takes the form
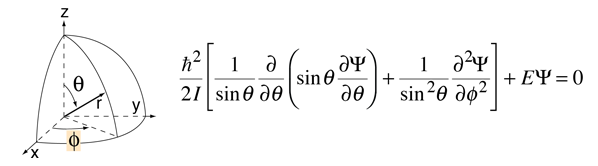
This form of the angular momentum contribution is also encountered in the solution of the Schrodinger equation for the hydrogen atom. The approach to the solution of this differential equation is to separate the variables in the form
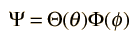
Substitution into the Schrodinger equation gives the two separated equations

where M is inserted as an arbitrary "separation constant" at this point, but will be found to represent MJ, the z-component of the angular momentum. Solutions to these equations which meet the necessary constraints on the wavefunction, i.e. single valued and normalizable, can be obtained only when
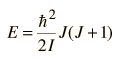
where J is a positive integer and M is an integer such that the absolute value of M is less than or equal to J.
The wavefunctions associated with these allowed solutions are
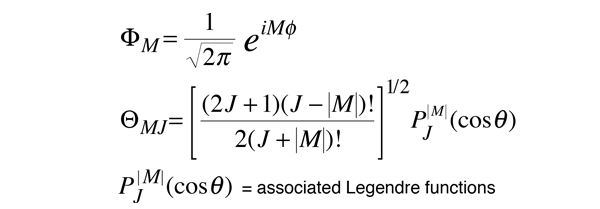
| Table of associated Legendre functions |
It is customary to define a rotational constant B for the molecule

so that the solutions for the energy states of a rigid rotator can be expressed as

In this context, the association M=MJ is made and the projections of the rotational angular momentum along the polar axis (z-axis) can be expressed as
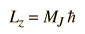
The rotational energy levels are normally degenerate with respect to MJ, but when there are perturbing influences like the application of an electric field (Stark effect), the levels are split into energy levels which depend upon MJ .
For a general rigid rotor with rotations about three principal axes, the energy can be expressed in terms of three rotational constants A, B, C, but the expressions for the energies become more complex. As an example, see the expressions for some lower energy states of the molecule SPF2H.
| Diatomic molecules |
| Determining the structure of a diatomic molecule |
| Determining the structure of a linear molecule |
| Example of the structure of a polyatomic molecule |
Molecular spectra concepts
| HyperPhysics***** Quantum Physics | R Nave |