Molecular Structure from Rotational Spectra

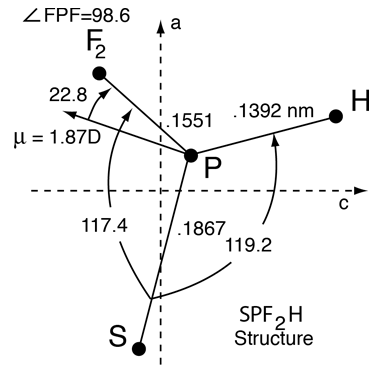
Suppose you are interested in the structure of a molecule like hydrothiophosphoryl difluoride, shown below. The most accurate way to determine the molecular structure of a molecule in the gas phase is by analysis of the rotational spectrum.

Determining rotational constants

In concept, the story of molecular structure determination starts with the expression for the rotational kinetic energy of a rigid rotator: 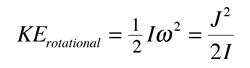When this is applied to a simple diatomic or linear molecule, this kinetic energy expression leads you to the quantum mechanical Hamiltonian which gives energy eigenvalues.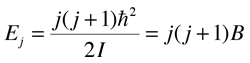

The parameter B is called the rotational constant and it is convenient to analyze the rotational spectrum in terms of this rotational constant. The analysis of the spectrum gives you a value for I and that lets you calculate the bond length for a diatomic molecule (see example for HCl).

For a general molecule there are three non-equivalent moments of inertia and the kinetic energy expression becomes

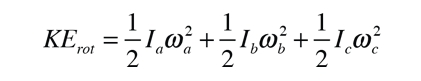
and the energies are expressed in terms of three rotational constants A, B and C.

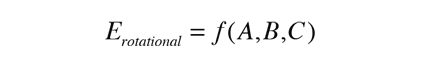
The complexity of the energy expressions is bad news in terms of the difficulty of analysis, but good news in terms of the information obtained. The structure of a diatomic molecule has only one unknown, but when you have multiple bond lengths and angles, you have several unknowns and need several equations to solve for them.

To determine the structure of SPF₂H, you have to determine three angles and three bond lengths, so you need six equations. Rotation about three non-equivalent axes gives you three. So how do you determine the structure?

The physical idea which rescues you from the dilemma of insufficient data is isotopic substitution. Since the bond lengths are determined by the electrostatic force, substituting a different isotope into the atom should not change the bond lengths since the electrical environment around the isotope is identical. However, the moments of inertia will be changed, giving you three more pieces of data in the form of the new rotational constants A', B', and C'.

While doing the experiment on SPF₂H, which has six structural parameters, it appeared that producing the molecule with deuterium substituted for normal hydrogen would be sufficient for structure determination since that would give you 6 parameters. We were working in a laboratory at the University College of North Wales in Bangor, Wales on a sample prepared by R. G. Cavell of the Department of Chemistry, Edmonton, Alberta. This was within months of the first time that compound had ever been synthesized; we had read of his initial synthesis. We contacted him and he graciously agreed to synthesize the molecule with deuterium substituted for hydrogen. The molecule is quite unstable and explosive on contact with air, so we treated the deuterated sample with great care and took data on its spectrum for about two weeks. Unfortunately, one night the glass vacuum system developed a leak and we came in the next morning to find it had exploded and we had lost both the sample and the vacuum system. At least we had two weeks of spectra and had enough data to determine the rotational constants.

Unfortunately, our consolation about having collected just enough data to determine the parameters of the deuterated species of the molecule was short-lived as we faced yet another hurdle to the determination of the molecular structure. Six pieces of data were not enough to determine the structure of this molecule! There is a plane of symmetry in this molecule, the two fluorines being at mirror image sites on each side of the plane formed by the SPH framework. This meant that once the two moments of inertia in the SPH plane were determined, the third moment of inertia was determined by the perpendicular axis theorem and not independent of the other two moments of inertia. Six independent pieces of data were required to calculate the structure unambiguously, and now we had only four.

We were rescued in this effort by the fact that the spectrum of SPF₂H was extremely strong and well resolved and we could in fact collect data for a third isotopic species, the species with sulfur-34. It has a natural abundance of 3% and this turned out to be enough to detect it. We knew where to look because we could make a fairly accurate model from the normal and deuterated sample data, and we still had the original sample. Solving for moments of inertia from our model, we predicted the locations of a dozen or so critical lines and looked for them at high resolution. The third set of rotational constants A",B", and C" gave us the needed data to calculate the structure shown.