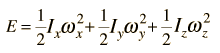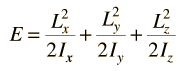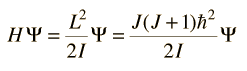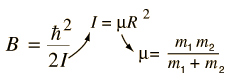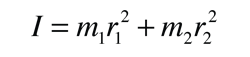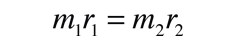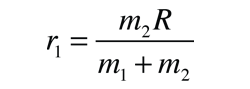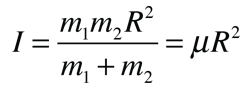Rotational Spectra

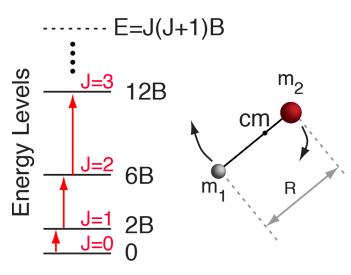
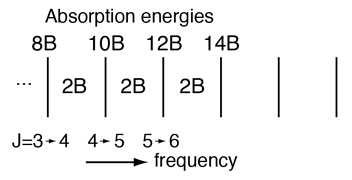
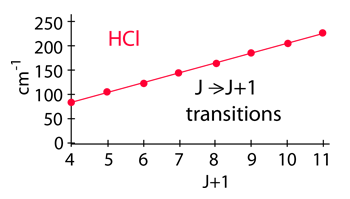
Incident electromagnetic waves can excite the rotational levels of molecules provided they have an electric dipole moment. The electromagnetic field exerts a torque on the molecule. The spectra for rotational transitions of molecules is typically in the microwave region of the electromagnetic spectrum. The rotational energies for rigid molecules can be found with the aid of the Shrodinger equation. The diatomic molecule can serve as an example of how the determined moments of inertia can be used to calculate bond lengths.

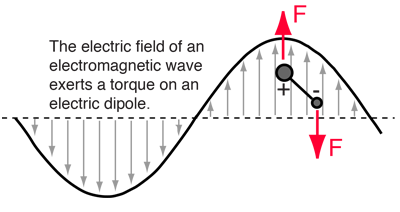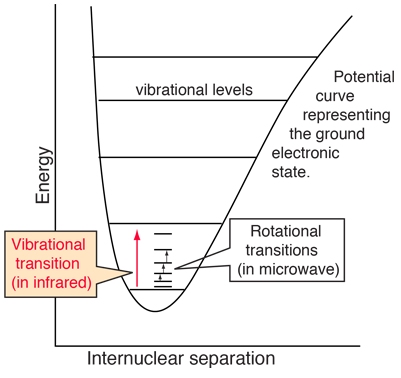The illustration at left shows some perspective about the nature of rotational transitions. The diagram shows a portion of the potential diagram for a stable electronic state of a diatomic molecule. That electronic state will have several vibrational states associated with it, so that vibrational spectra can be observed. Most commonly, rotational transitions which are associated with the ground vibrational state are observed.

Rotational Energies

The classical energy of a freely rotating molecule can be expressed as rotational kinetic energy

where x, y, and z are the principal axes of rotation and I_x represents the moment of inertia about the x-axis, etc. In terms of the angular momenta about the principal axes, the expression becomes

The formation of the Hamiltonian for a freely rotating molecule is accomplished by simply replacing the angular momenta with the corresponding quantum mechanical operators.

Diatomic Molecules

For a diatomic molecule the rotational energy is obtained from the Schrodinger equation with the Hamiltonian expressed in terms of the angular momentum operator.

More detail

where J is the rotational angular momentum quantum number and I is the moment of inertia.

Rotational transitions

Determining the rotational constant B enables you to calculate the bond length R. The allowed transitions for the diatomic molecule are regularly spaced at interval 2B. The measurement and identification of one spectral line allows one to calculate the moment of inertia and then the bond length.

Rotational Transitions, Diatomic

For a rigid rotor diatomic molecule, the selection rules for rotational transitions are ΔJ = +/-1, ΔM_J = 0 .

	The rotational spectrum of a diatomic molecule consists of a series of equally spaced absorption lines, typically in the microwave region of the electromagnetic spectrum. The energies of the spectral lines are 2(J+1)B for the transitions J -> J+1.
	For real molecules like the example of HCl , the successive transitions are a bit lower than predicted because centrifugal distortion lengthens the molecule, increasing its moment of inertia.

Moment of Inertia, Diatomic

The moment of inertia about the center of mass is From the center of mass definition and substituting to eliminate r1 and r2 gives where μ is called the "reduced mass."