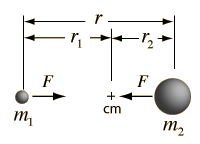
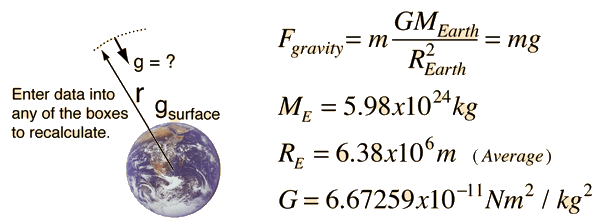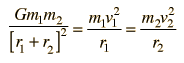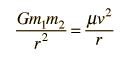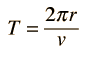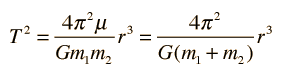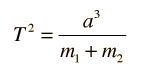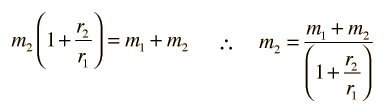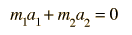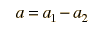Circular Orbit
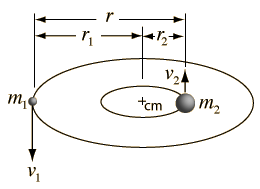
Gravity supplies the necessary centripetal force to hold a satellite in orbit about the earth. The circular orbit is a special case since orbits are generally ellipses, or hyperbolas in the case of objects which are merely deflected by the planet's gravity but not captured. Setting the gravity force from the universal law of gravity equal to the required centripetal force yields the description of the orbit. The orbit can be expressed in terms of the acceleration of gravity at the orbit.
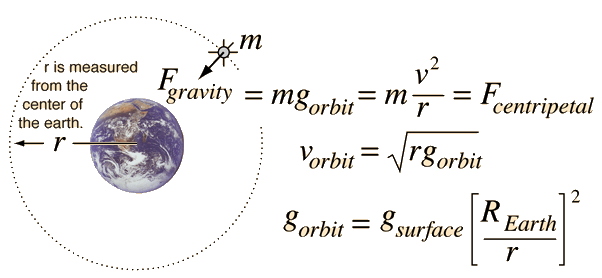
The force of gravity in keeping an object in circular motion is an example of centripetal force. Since it acts always perpendicular to the motion, gravity does not do work on the orbiting object if it is in a circular orbit.
Calculation |
Gravity concepts
Orbit concepts
| HyperPhysics***** Mechanics ***** Rotation | R Nave |