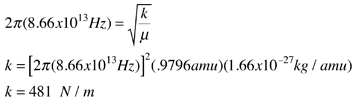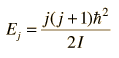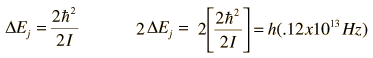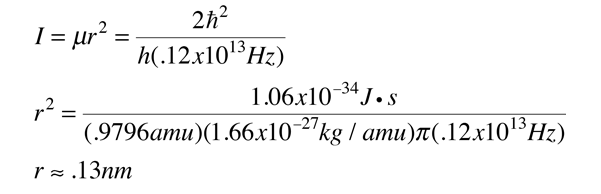Vibration-Rotation Spectrum of HCl
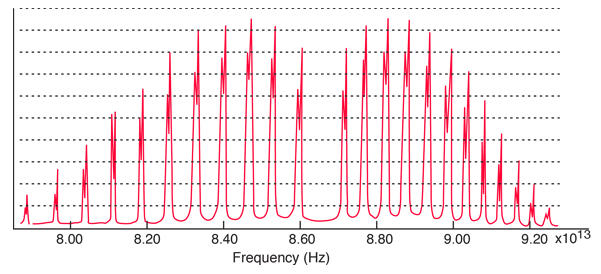
A classic among molecular spectra, the infrared absorption spectrum of HCl can be analyzed to gain information about both rotation and vibration of the molecule.
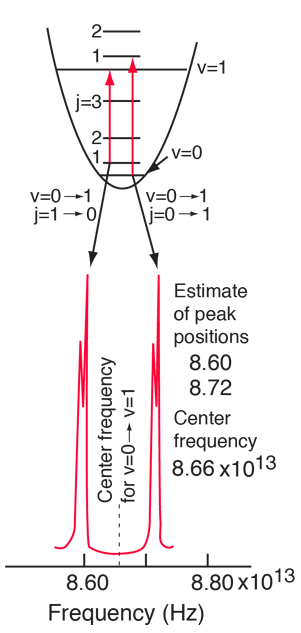
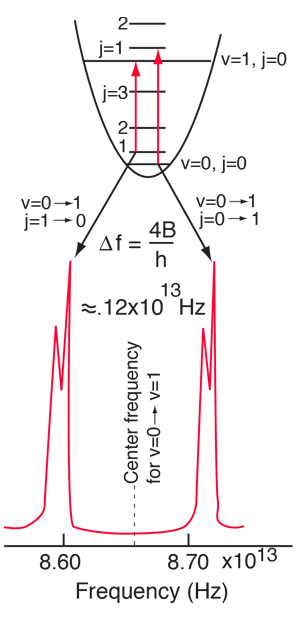
The absorption lines shown involve transitions from the ground to first excited vibrational state of HCl, but also involve changes in the rotational state. The rotational angular momentum changes by 1 during such transitions. If you had a transition from j=0 in the ground vibrational state to j=0 in the first excited state, it would produce a line at the vibrational transition energy. As observed, you get a closely spaced series of lines going upward and downward from that vibrational level difference. The splitting of the lines shows the difference in rotational inertia of the two chlorine isotopes Cl-35(75.5%) and Cl-37(24.5%).
From the spectrum above, you can examine details about the following:
|
|
|
|
|
|
|
|
|
|
Molecular spectra concepts
Reference
Tipler & Llewellyn
Sec. 9-4
| HyperPhysics***** Quantum Physics | R Nave |