Quantum Harmonic Oscillator
A diatomic molecule vibrates somewhat like two masses on a spring with a potential energy that depends upon the square of the displacement from equilibrium. But the energy levels are quantized at equally spaced values.
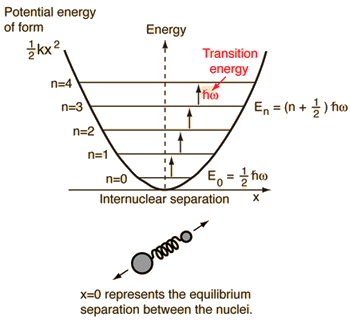 |
The energy levels of the quantum harmonic oscillator are  and for a diatomic molecule the natural frequency is of the form  where the reduced mass is given by 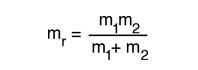 |
This form of the frequency is the same as that for the classical simple harmonic oscillator. The most surprising difference for the quantum case is the so-called "zero-point vibration" of the n=0 ground state. This implies that molecules are not completely at rest, even at absolute zero temperature.
The quantum harmonic oscillator has implications far beyond the simple diatomic molecule. It is the foundation for the understanding of complex modes of vibration in larger molecules, the motion of atoms in a solid lattice, the theory of heat capacity, etc. In real systems, energy spacings are equal only for the lowest levels where the potential is a good approximation of the "mass on a spring" type harmonic potential. The anharmonic terms which appear in the potential for a diatomic molecule are useful for mapping the detailed potential of such systems.
| Schrodinger equation for harmonic oscillator | Wavefunctions |
| Correspondence principle | Probability distributions |
Schrodinger equation concepts
References
Beiser, Perspectives
Sec 8-7
Blatt
Sec 7-9
| HyperPhysics***** Quantum Physics | R Nave |