The Correspondence Principle and the Quantum Oscillator

Quantum mechanics is necessary for the description of nature on the atomic scale, but Newton's laws do fine for baseballs. Somewhere along the continuum from quantum to classical, the two descriptions must merge. Starting from the quantum end and noting that energies depend upon some quantum number, one would anticipate that for high enough quantum numbers, the quantum treatment should merge with the classical. This idea of the merging of the quantum and classical is called the "correspondence principle"

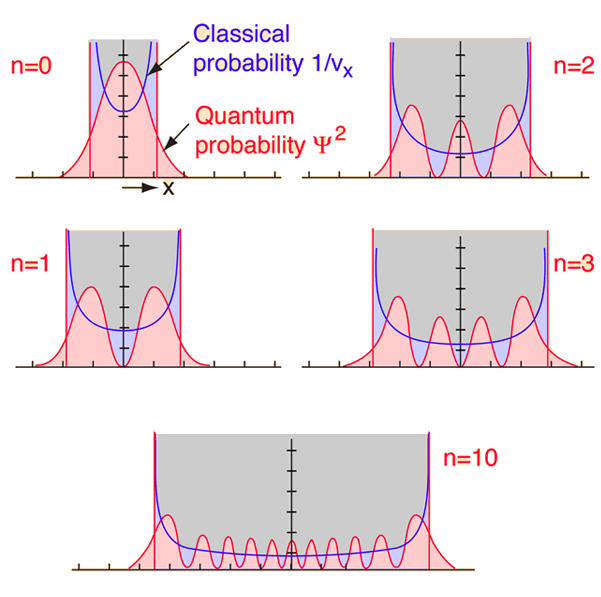
If you examine the ground state of the quantum harmonic oscillator, the correspondence principle seems far-fetched, since the classical and quantum predictions for the most probable location are in total contradiction. If the equilibrium position for the oscillator is taken to be x=0, then the quantum oscillator predicts that for the ground state, the oscillator will spend most of its time near that center point. The classical mass-on-a-spring will obviously spend very little time there because it has the maximum speed there; it will spend most of its time near the end points of its oscillation where its velocity is small.

As you go to higher and higher states of the quantum oscillator by increasing n, the most probable location shifts to the outside of the well. You still have the undulation of the probability which is characteristic of the wave solution, but at least the overall trend of the probability begins to look more like the classical probability which is shown by the dashed line.
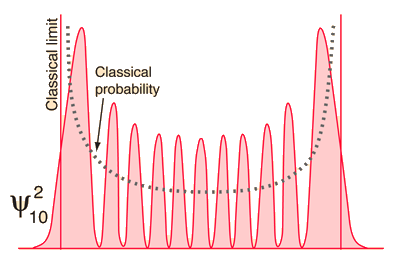This wild oscillation of the probability has practical consequences only if it is observable, and the higher the quantum number, the smaller the distance between peaks. At high enough n, the uncertainty principle will prevent you from resolving the gaps without altering the physical state of the oscillator. The exponential tails into the classically forbidden region decrease with increasing n, so the quantum oscillator looks more and more like the classical one.

Bohr used the term "correspondence principle" and expected that the radiative behavior of atoms would approach the classical radiation from accelerated charges for high enough quantum states. Certainly the observed line spectra from atoms differ radically from classical behavior. Beiser gives an example of calculating the radiation frequency of an atom for quantum number n=10,000 and states that it differs from the classical result by only 0.01%.

Further detail about classical and quantum probabilities
 Index

Schrodinger equation concepts

References
Beiser, Perspectives
Sec 6-6
Thornton & Rex
Sec 7-6, 8-7
 
HyperPhysics***** Quantum Physics R Nave
 Go Back





Comparison of Classical and Quantum Probabilities for Harmonic Oscillator

The harmonic oscillator is an important problem in both the quantum and classical realm. It is also a good example of how different quantum and classical results can be. One type of comparison is that of the probability of finding the object which is oscillating at a given distance x from the equilibrium position. For the classical case, the probability is greatest at the ends of the motion since it is moving more slowly and comes to rest instantaneously at the extremes of the motion. The relative probability of finding it in any interval Dx is just the inverse of its average velocity over that interval. For the quantum mechanical case the probability of finding the oscillator in an interval Dx is the square of the wavefunction, and that is very different for the lower energy states. Note from the diagram for the ground state (n=0) below that the maximum probability is at the equilibrium point x=0.

For the first few quantum energy levels, one can see little resemblance between the quantum and classical probabilities, but when you reach the value n=10 there begins to be some similarity. To be sure, they don't look the same, but they do agree that the probability is greatest near the ends of the motion. As you proceed to very high n values, they become more and more alike, and the oscillations of the quantum probability become so close together that they are practically smeared together. The fact that the overall picture of probability of finding the oscillator at a given value of x converges for the quantum and classical pictures is called the correspondence principle.

Another thing to note about the classical and quantum probabilities above is that the classical probability is strictly contained between the vertical lines which represent the classical limit. The quantum probabilities do extend into the classically forbidden region, exponentially decaying into that region.

Probabilities superimposed on oscillator potential
 Index

Schrodinger equation concepts

Reference
Blatt
Ch 7
 
HyperPhysics***** Quantum Physics R Nave
 Go Back