Determining the Rotational Constants
The rotational spectrum of a typical asymmetric top molecule is a forest of lines in any given frequency range, with high-J lines mixed with low-J lines. Sorting them out is sometimes a very difficult puzzle. But some of the lines must be identified with their rotational quantum numbers before any progress can be made toward structure determination. A common procedure is to model the molecule with your best information about what the bond lengths and angles should be and calculate the frequency of certain critical low-J rotational transitions. Then with a rotational (microwave) spectrometer, you look for the characteristic Stark effects which signal low-J transitions.
For the example of the molecule SPF2H, we were fortunate enough to be able to measure several J=1->2 transitions, which permit a rather straightforward calculation of the rotational constants. Dipole moment components along the different principal axes a,b and c give particular selection rules for transitions. A fortuitous combination of transitions and the rotational constants calculated from them are shown below.
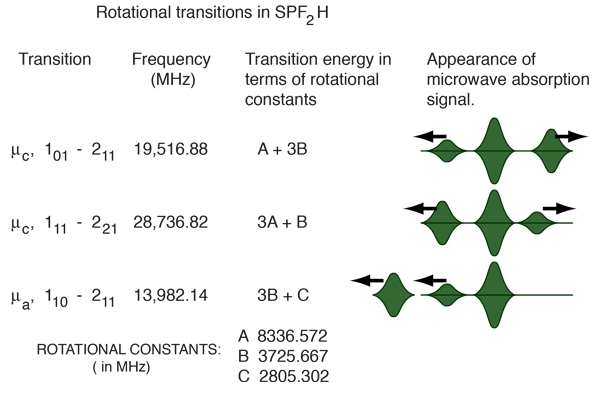
To paint a little more accurate picture of the final process, the quoted rotational constants in the illustration above were determined by a least squares fit of 71 transitions after the effects of centrifugal distortion on the rotational transition frequencies had been modeled. Finding values for the rotational constants from just the above transitions would allow you to fit these three transitions more accurately, but fitting 71 transitions gave a better overall fit and permitted the modeling of the centrifugal stretching of the bonds as a result of the rotation.
|
|
Molecular spectra concepts
References
Nave & Sheridan
Cavell
| HyperPhysics***** Quantum Physics | R Nave |