Legendre Polynomials

One of the varieties of special functions which are encountered in the solution of physical problems is the class of functions called Legendre polynomials. They are solutions to a very important differential equation, the Legendre equation:

The polynomials may be denoted by Pn(x) , called the Legendre polynomial of order n. The polynomials are either even or odd functions of x for even or odd orders n. The first few polynomials are shown below.

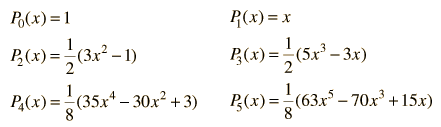
The general form of a Legendre polynomial of order n is given by the sum:

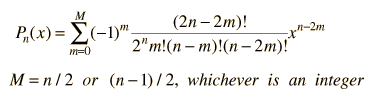
From the Legendre polynomials can be generated another important class of functions for physical problems, the associated Legendre functions.

The equation takes its name from Adrien Marie Legendre (1752-1833), a French mathematician who became a professor in Paris in 1775. He made important contributions to special functions, elliptic integrals, number theory, and the calculus of variations. (Kreyszig).

Index

Reference
Kreyszig
Sec 4.3
 
HyperPhysics*****HyperMath*****CalculusR Nave
 Go Back





Associated Legendre Functions

An important class of special functions called the associated Legendre functions can be derived from the Legendre polynomials. The defining relationship is

where Pn(x) is the Legendre polynomial of order n. These functions are of great importance in quantum physics because they appear in the solutions of the Schrodinger equation in spherical polar coordinates. In that context the variable x is replaced by cosq, where q is the colatitude angle. Also in that context, the wavefunctions which are the solutions of the Schrodinger equation need to be normalized, so the list of functions below will include the normalization factor

The normalized functions are of the form

and appear in the wavefunctions for the hydrogen atom. The first few normalized associated Legendre functions are listed below.

The associated Legendre functions can be used to construct another important set of functions, the spherical harmonics.

Index

References
Kreyszig
Sec 4.3

Leighton
Ch 5
 
HyperPhysics*****HyperMath*****CalculusR Nave
 Go Back