Vector Model for Orbital Angular Momentum

The orbital angular momentum for an atomic electron can be visualized in terms of a vector model where the angular momentum vector is seen as precessing about a direction in space. While the angular momentum vector has the magnitude shown, only a maximum of l units can be measured along a given direction, where l is the orbital quantum number. Since there is a magnetic moment associated with the orbital angular momentum, the precession can be compared to the precession of a classical magnetic moment caused by the torque exerted by a magnetic field. This precession is called Larmor precession and has a characteristic frequency called the Larmor frequency.

While called a "vector", it is a special kind of vector because its projection along a direction in space is quantized to values one unit of angular momentum apart. The diagram shows that the possible values for the "magnetic quantum number ml for l=2 can take the values = -2, -1, 0, 1, 2 or, in general = -l, -l+1,..., l-1, l .

Vector Model for Total Angular Momentum

When orbital angular momentum L and electron spin angular momentum S are combined to produce the total angular momentum of an atomic electron, the combination process can be visualized in terms of a vector model. Both the orbital and spin angular momentua are seen as precessing about the direction of the total angular momentum J. This diagram can be seen as describing a single electron, or multiple electrons for which the spin and orbital angular momenta have been combined to produce composite angular momenta S and L respectively. In so doing, one has made assumptions about the coupling of the angular momenta which are described by the L-S coupling scheme which is appropriate for light atoms with relatively small external magnetic fields.

The combination is a special kind of vector addition as is illustrated for the single electron case l=1 and s=1/2. As in the case of the orbital angular momentum alone, the projection of the total angular momentum along a direction in space is quantized to values differeing by one unit of angular momentum.

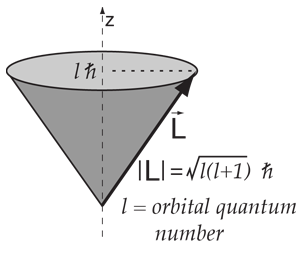
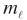Angular Momentum in a Magnetic Field

Once you have combined orbital and spin angular momenta according to the vector model, the resulting total angular momentum can be visuallized as precessing about any externally applied magnetic field.

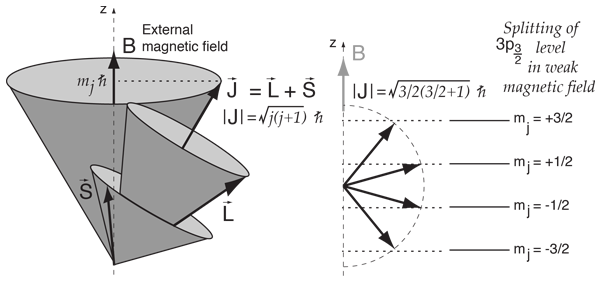
This is a useful model for dealing with interactions such as the Zeeman effect in sodium. The magnetic energy contribution is proportional to the component of total angular momentum along the direction of the magnetic field, which is usually defined as the z-direction.

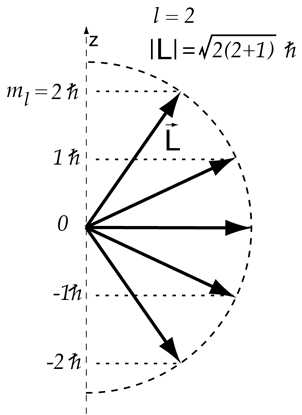
The z-component of angular momentum is quantized in values one unit apart, so for the upper level of the sodium doublet with j=3/2, the vector model gives the splitting shown.

Even with the vector model, the determination of the magnitude of the Zeeman spliting is not trivial since the directions of S and L ar constantly changing as they precess about J. This problem is handled with the Lande' g-factor.

This treatment of the angular momentum is appropriate for weak external magnetic fields where the coupling between the spin and orbital angular momenta can be presumed to be stronger than the coupling to the external field. This can be visualized with the help of a vector model of total angular momentum. If the external field is very strong, then it can decouple the spin and orbital angular momenta. This strong field case is called the Paschen-Back effect and leads to different patterns of splitting of the energy levels.