Derivatives and Integrals
Foundational working tools in calculus, the derivative and integral permeate all aspects of modeling nature in the physical sciences.
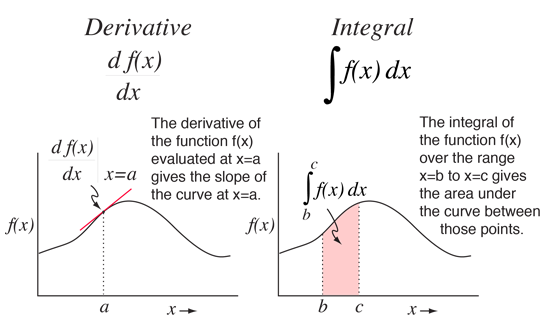
The derivative of a function can be geometrically interpreted as the slope of the curve of the mathematical function f(x) plotted as a function of x. But its implications for the modeling of nature go far deeper than this simple geometric application might imply. After all, you can see yourself drawing finite triangles to discover slope, so why is the derivative so important? Its importance lies in the fact that many physical entities such as velocity, acceleration, force and so on are defined as instantaneous rates of change of some other quantity. The derivative can give you a precise intantaneous value for that rate of change and lead to precise modeling of the desired quantity.
The integral of a function can be geometrically interpreted as the area under the curve of the mathematical function f(x) plotted as a function of x. You can see yourself drawing a large number of blocks to appproximate the area under a complex curve, getting a better answer if you use more blocks. The integral gives you a mathematical way of drawing an infinite number of blocks and getting a precise analytical expression for the area. That's very important for geometry - and profoundly important for the physical sciences where the definitions of many physical entities can be cast in a mathematical form like the area under a curve. The area of a little block under the curve can be thought of as the width of the strip weighted by (i.e., multiplied by) the height of the strip. Many properties of continuous bodies depend upon weighted sums, which to be exact must be infinite weighted sums - a problem tailor-made for the integral. For example, finding the center of mass of a continuous body involves weighting each element of mass by its distance from an axis of rotation, a process for which the integral is necessary if you are going to get a precise value. A vast number of physical problems involve such infinite sums in their solutions, making the integral an essential tool for the physical scientist.
Derivative concepts
Integral concepts
| HyperPhysics*****HyperMath*****Calculus | R Nave |