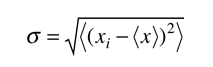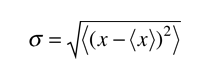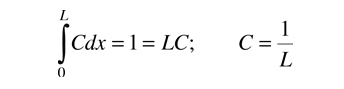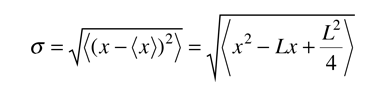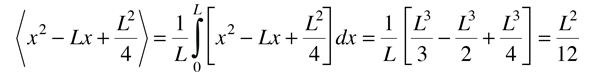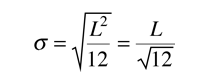The Standard Deviation for Discrete Measurements
In many cases, physical measurements in a context which involves probability will form a collection of results which can be approximated by a normal distribution. In such cases a large number of experimental results will form a gaussian curve. Consider first an example in which we have a complete set of measurements which is often called a "population". It is useful to calculate the standard deviation from the mean of the population measurements. For a population of N we can determine the mean μ = < x > of the measurements x and the variance σ2 of the deviations from the mean. The standard deviation σ is the square root of the variance.
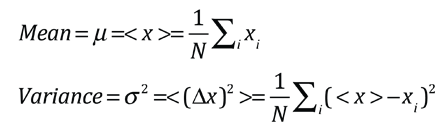
The Standard Deviation from a Sample Mean
For an experimental situation in which neither the population N nor it's mean are known, a sample of n measurements can be used to compute an estimate of the population mean.
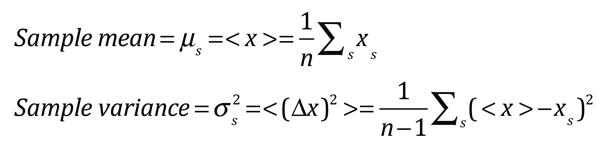
The calculated values of the mean μs and standard deviation σs from that sample mean may be taken as estimates of the corresponding values for the population, which are unknown. The question that arises is "why n-1 rather than n in the sample variance expression?" Savory points out that since the variance σs2 is measured with deviations from the sample average rather than the population average, the deviations tend to be smaller than the deviations from the population mean. Using n-1 rather than n tends to correct for the bias in the estimate of the variance. An empirical example of the effect of the n-1 correction is posted by Khan Academy.
Another point in this discussion is that the deviation values for the sample are based on the sample average rather than the population average. So once you have determined n-1 independent values in the sample measurements based on that average, the last deviation value is predetermined and not independent.
As a formal discussion of sample statistics, this approach to a partial correction of sample bias is known as Bessel's correction after Friedrich Bessel.
| Standard deviation using a distribution function |
Applied statistics concepts
Rohlf
Sec 2.1
Kreyzig
22.1, 23.2
Savory
Bessel's correction
Khan Academy example
| HyperPhysics*****HyperMath*****Algebra | R Nave |