Journey through the center of the Earth
 |
Suppose you could drill a hole through the Earth and then drop into it. How long would it take you to pop up on the other side of the Earth? |
Your initial acceleration would be the surface acceleration of gravity
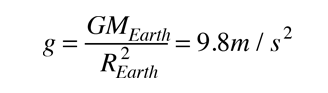
but the acceleration would be progressively smaller as you approached the center. Your weight would be zero as you flew through the center of the Earth. For our hypothetical journey we will assume the Earth to be of uniform density and neglect air friction and the high temperature of this trip.
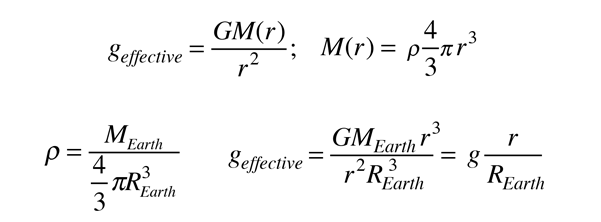
 | For a spherically symmetric mass, the net gravity force on an object from that mass would be only that due to the mass inside its radius, and that would act as if it were a point mass located at the center. When this is analyzed in detail, you find that the gravity at any radius r less than REarth will be linearly proportional to the distance from the center. |
| Gravity force of spherical shell | On mass outside the shell |
| On mass inside the shell |
Taking positive r as outward from the center of the Earth:
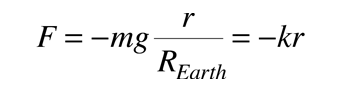
This is the same form as Hooke's Law for a mass on a spring. It would cause the trans-Earth traveler to oscillate back and forth through the center of the Earth like a mass bobbing up and down on a spring. The angular frequency and period for this oscillation are

For this case the period of oscillation is
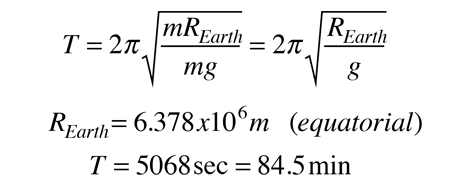
The traveler accelerates toward the center of the Earth and is momentarily weightless when passing through the geometric center at about 7900 m/s or almost 17,700 miles/hr. The traveler would pop up on the opposite side of the Earth after a little more than 42 minutes. But unless he or she grabs something to hold on, they will fall back for a return journey and continue to oscillate with a round-trip time of 84.5 minutes.
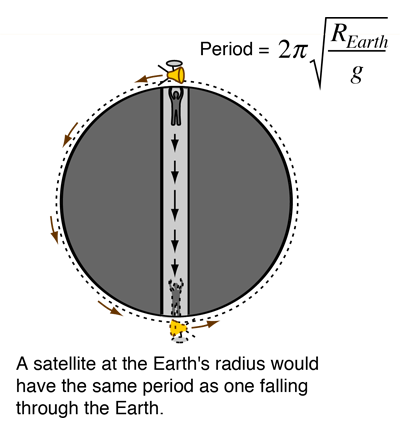 | As a further feature of this fanciful journey, suppose a satellite could be put in a circular orbit about the Earth right above the surface. Ignoring air drag and the terrific sonic boom that would accompany such an orbit, suppose it passed overhead just above the falling person as they popped up out of the hole. The period of such an orbit would be such that it would be passing overhead every time the oscillating person popped up on either side of the Earth. |
The period of the orbit is calculated from

which is the same as the period of the oscillating body.
Sanity check on the hole-through-the-Earth example
OK, if you have analyzed this example, you might well have observed that the forward momentum of the dropped object relative to the center of mass of the Earth would mean that it would almost immediately collide with the forward wall of the hole, so the whole example is really a swindle in terms of what would happen in the real world. So for this to work, the dropped object would have to bounce elastically off the front and rear walls, and would be oscillating back and forth very rapidly as it approached the center of the earth. After all, your initial horizontal speed is nominally 465 m/s relative to the center, using an equatorial radius, so that gives a fairly rapid oscillation back and forth between the walls of our idealized well as you approach the center. Neglecting the fact of how hot the center is, and the fact that your object would melt, and your hole would close - Oh, well, this is all silliness to begin with. But blithely proceeding in the face of real-world facts, if you maintained the hole and the elastic collisions, things would get more extreme on the way up toward the opposite side of the Earth since the elastic presumption would imply that the velocity perpendicular to the radius would approach twice the 465 m/s, so if the object emerged from the hole, it would go zinging off at 930 m/s, almost mach 3. So it's best not to stand close to the hole.
So the hole through the center of the Earth really doesn't work, but this example has generated some interesting comments. Having swept all these difficulties under the rug in posting this example, it yet gives some interesting correlations to orbital velocities and surprisingly to Hooke's law.
| Other examples of weightlessness |
Newton's laws
Gravity concepts
| HyperPhysics***** Mechanics | R Nave |