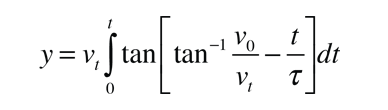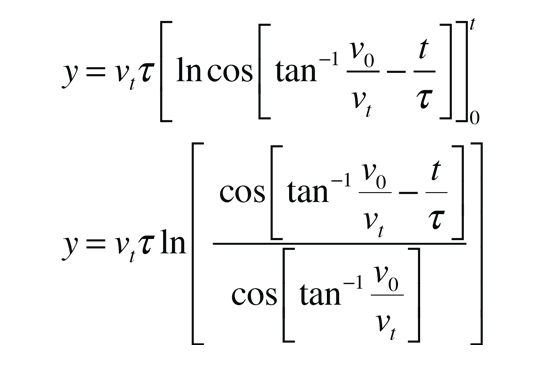Time to Peak for Quadratic Drag
A vertically launched object will be presumed to experience an air resistance force proportional to the square of its speed. For a launch speed of v0 the object is to calculate the time to the peak. The expressions will be developed for the two forms of air drag which will be used for trajectories:
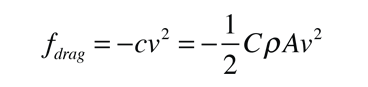
but the simpler -cv2 form will be used initially for simplicity and the forms for terminal velocity vt and characteristic time τ will be used.
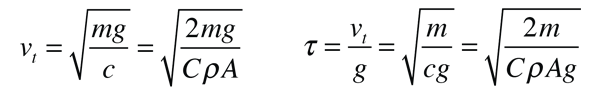
The motion equation for this vertical launch is

which can be integrated for time t in the form

but this is a non-trivial integral. Using an integral table it can be expressed as
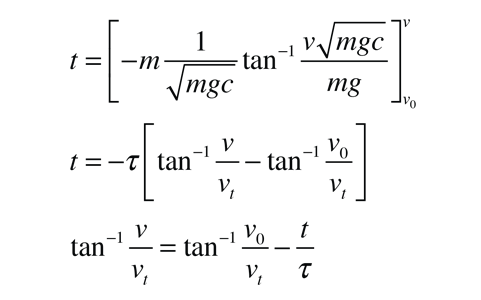
We finally reach an expression for the velocity as a function of time:
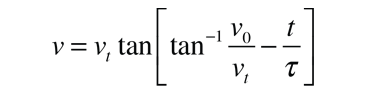
Now to find the time at the peak of the vertical trajectory, we can set the velocity equal to zero, yielding

This expression is used in the vertical trajectory calculation.
Fluid friction
Reference
A. Douglas Davis
Sec. 2.6
| HyperPhysics***** Mechanics ***** Fluids | R Nave |