Musical Scales
Background Material for Tuning and Temperament
assumptions about the human hearing process:
- The ear is sensitive to ratios of frequencies (pitches) rather than to differences in establishing musical intervals.
- The intervals which are perceived to be most consonant are composed of small integer ratios of frequency.

|
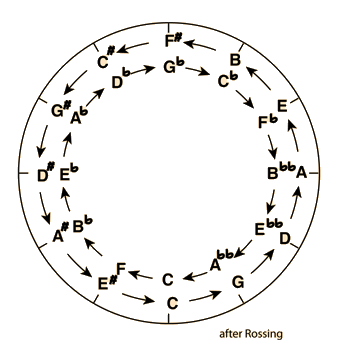
The octave, fifth, and fourth are the intervals which have been considered to be consonant throughout history by essentially all cultures, so they form a logical base for the building up of musical scales. A typical strategy for using these univerally consonant intervals is the circle of fifths. |
Temperament and musical scales
| HyperPhysics***** Sound | R Nave |