The Value of the Cross-Section Concept
If you are firing projectiles which you cannot see at targets which are much smaller than atoms, how can you make sense out of what you detect on the other side of the target? This kind of scenario highlights the value of the concept of cross-section.
If you had a uniform beam of projectiles and encountered a target which intercepted 1% of the area of the beam, you would expect 1% of the projectiles to be scattered. That basic concept can be extended to the calculation of the fraction of alpha particles scattered from a gold foil.
Suppose you had a beam of incident alpha particles with rate Ri = 10,000 /s on a gold foil of thickness 10-6 meters and the effective area (cross-section) for each gold nucleus was 100 barns. The fraction of those 10,000 particles scattered would be the fraction of the beam area which is covered by one of the scattering gold nuclei. The fraction of the beam covered can be calculated as follows

Multiplying the number of targets per square meter times the cross-section for each target gives you the fraction of the area which is covered by target and therefore the fraction of the beam which would be scattered:

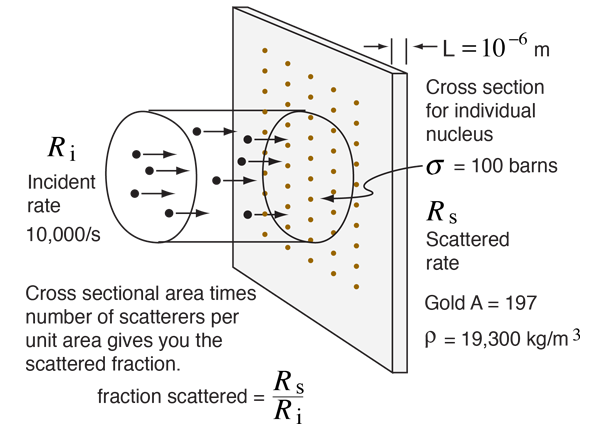

For an incident rate of 10,000/s, an average of 5.88 particles/s would be expected to be scattered.
To put this example more directly in the context of Rutherford scattering, you can use the cross-section calculation to verify that for 6 MeV alpha particles incident upon this gold film, the cross-section would be 100 barns for scattering above about 37 degrees. Another context would be the calculation of scattering within an angular window. For example, suppose you start at 20 degrees, where the calculated cross-section is 363 barns for scattering above that angle. The scattering cross-section for scattering at 23.4 degrees is about 263 barns, so the cross-section for scattering between 20 and 23.4 degrees is about 100 barns. Using finite detectors and windows like this, the Rutherford team was able to compare the number of scattered alpha particles at different scattering angles and confirm that they followed the calculated pattern for coulomb scattering. Then at higher energies, when they detected a departure from the pattern, they could judge that they had interacted with a different kind of force (the strong force) and could then imply a radius for the nucleus.
Rutherford concepts
| HyperPhysics***** Nuclear | R Nave |