Impact Parameter for Nuclear Scattering
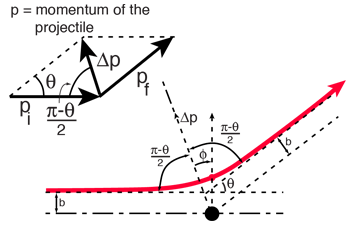 |
For scattering under the influence of the Coulomb force, the angle of scattering is related to the impact parameter b illustrated at left. Under the assumption that the target recoil is negligible, the change in momentum associated with the scattering is 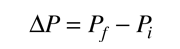 where the magnitudes of the initial and final momenta are the same. |
The scattering geometry gives
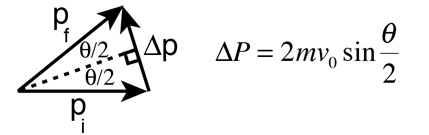
One way to obtain an expression for the change in momentum is to use the concept of impulse of force and the symmetry of the scattering geometry. Only the impulse component along the symmetry axis of the hyperbola will produce a net momentum change. Therefore
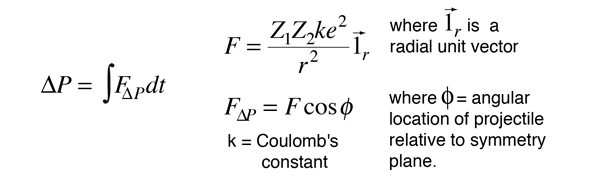
This gives

Conservation of angular momentum can be used to advantage in evaluating the impulse integral.
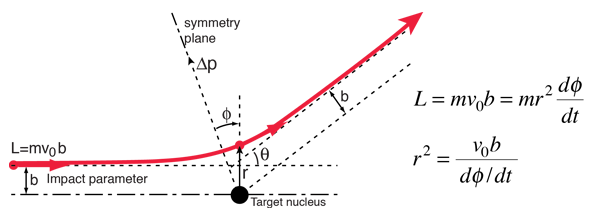
Here we have used the expression for the angular momentum of a particle and the fact that it can be expressed as the product of mass, radius, and velocity perpendicular to the radius at any point on the hyperbolic path. Substitution gives
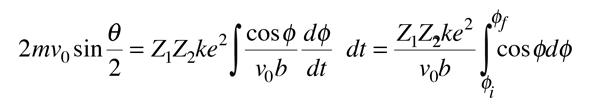
Extending the entrance and exit paths of the scattering trajectory to infinity gives the limits on the angle:
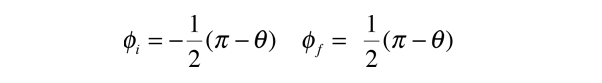
Using the angle difference identity puts the integral in the form

Solving for the impact parameter b gives
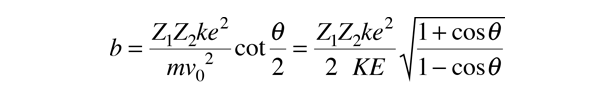
The two forms above can be shown to be equivalent using the half-angle identities. In this expression k is Coulomb's constant, e the electron charge and KE is the kinetic energy of the projectile particle.
| Calculation of impact parameter and closest approach |
Rutherford concepts
| HyperPhysics***** Nuclear | R Nave |