Overview of Resonant Systems
Physics 4060- Acoustics Laboratory
This lab is designed to make sure the student has some exposure to the basic classes of resonant acoustic systems. A resonant frequency is defined as a natural frequency of vibration determined by the physical properties of the vibrating object. The following experimental tests involve measuring the resonant frequency, or using the known resonant frequency to determine some other property.
A. Vibrating string
The vibrating string is the basic example of the "standing wave" type of resonance. You should be aware that elastic waves travel up and down the string according to the basic wave relationship v = fl where v=velocity, f=frequency in Hz, and l=wavelength. The fixed ends of the string are constrained to be nodes, so the condition for resonance is

where L is the string length and n is any integer, i.e., the string produces a fundamental frequency (n=1) and all harmonics of that frequency.
For this part of the experiment, a metal string mounted on a wooden box called a sonometer will be used. Hang a sufficient amount of mass on the hanger to stretch the string to a reasonable tightness for producing a tone when plucked. Adjust the string supports for a convenient length of string. Hang a mass of 2 kg on the string and set up a microphone to pick up the sound of the string.
Find the fundamental resonant frequency of the string and record it. Use this frequency and the tension to calculate the mass per unit length of the string. Predict the frequency for a 3 kg suspended to tension the string and measure it for confirmation. Calculate the tension required to tune the string to C and measure it for comparison to the expected pitch.
B. Closed Cylindrical Air Column
Using the standard resonance tube apparatus with adjustable water level and a 440 Hz tuning fork, locate the fundamental and third harmonic resonances of the closed cylinder. Determine the speed of sound in the air in the tube. Note that the difference between the two resonant lengths should give the best wavelength determination since an end correction of about 0.6 x the radius of the tube must be applied at the open end if it is to be included in the measurement. Calculate the sound speed in m/sec and compare with the standard calculation of sound speed
v = 331.5 + 0.61 TC m/s.
C. Open Cylinder (Rijke tubes)
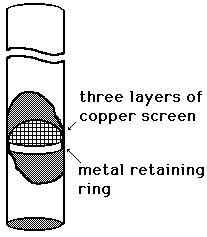
You will be provided with metal tubes which have a piece of copper gauze inserted in one end of the tube to a distance about one-fifth of the tube length. Hold the tube vertically over a bunsen burner flame so that the flame will heat the gauze to red heat. After holding the end of the tube over the flame for a few seconds, you can move it to one side and you should be able to hear the pipe sound its fundamental frequency. Using the microphone and a frequency counter, measure the frequency of the sound produced. If the sound is not strong enough to measure this way, you may have to use a storage scope for the frequency determination.
Compare the resonant frequency to the calculated resonant frequency at room temperature, including 0.6 x radius as an end correction for the length of the tube on each end. Assuming that the standard resonant frequency calculation is valid, calculate the effective temperature (Celsius) inside the tube when it is sounding.
D. Speed of Sound in Metal
Use the Kundt's tube apparatus to determine the velocity of sound in the metal rod. Instructions for the apparatus will be given, along with tips for the proper appreciation of its unique musical quality (bring ear plugs).
Stroking the metal rod with a rosin-coated cloth or skin produces longitudional waves in the rod. The vibrations of the small disc on the end of the rod produce sound waves in the air inside the glass tube, causing periodic ripple patterns in the cork dust in the tube. You will need to measure the wavelength of sound in the air, keeping in mind that the striated cork dust patterns represent antinodes and that the difference between successive antinodes is a half wavelength. You will need to measure the rod length to determine the wavelength of sound in the rod. The rod must be clamped precisely at its midpoint to vibrate properly. The rod may then be presumed to be vibrating in its fundamental longitudional mode (length = half wavelength).
To diminish the effect of end errors in the measurement of the wavelength in air, measure the overall length of as many patterns as possible and divide by the number of spaces to get a number for the half wavelength. Use the velocity of sound in air to determine the frequency of the sound.
Use the microphone and storage oscilloscope to get a frequency for the sound and compare it with the frequency you obtained from your wavelength measurement. Compare your speed of sound in the metal with a handbook value for that metal.
E. Resonance of an Air Cavity (Helmholtz Resonance)
Air cavities exhibit a single resonant frequency called a Helmholtz resonance. Such resonances are important for enhancing the tone of guitars, violins, and other string instruments. They are the absorbing frequencies of cavity type "bass traps" in studios. Tunable Helmholtz resonant cavities are used in bass-reflex type loudspeakers to enhance acoustic power and bass response (the ports you see on some loudspeakers are the openings to the Helmholtz resonators).
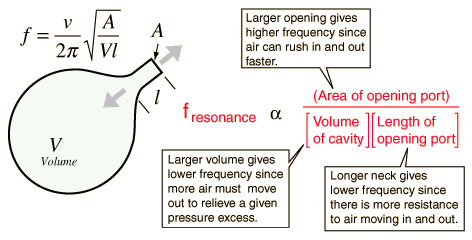
In this part of the experiment, you will use a carefully designed acoustic cavity which has been shown to exhibit a prominant Helmholtz resonance (an empty Coke bottle). Blow over the end and measure the resonant frequency. Using a graduated cylinder, add 50 cm3 of water to the bottle and remeasure the frequency. Continue this process until you have filled the bottle, recording the frequency and volume of water added. Once you have filled the bottle to determine its volume, you can calculate the air volume corresponding to each of your measured frequencies. Plot the frequency as a function of the inverse square root of the air volume .
Measure the area of the opening (the mouth of the coke bottle) and calculate an effective neck length from the relationship above. You can use an average value for the quantity 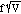 from your data.
from your data.
Physics 4060 Laboratory
Sound and Hearing