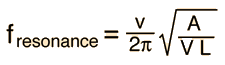Cavity Oscillations
The single frequency cavity resonance suggests a parallel with the single resonant frequency of a mass on a spring. In fact, the term "acoustic mass" is sometimes used in connection with such oscillations.
 |
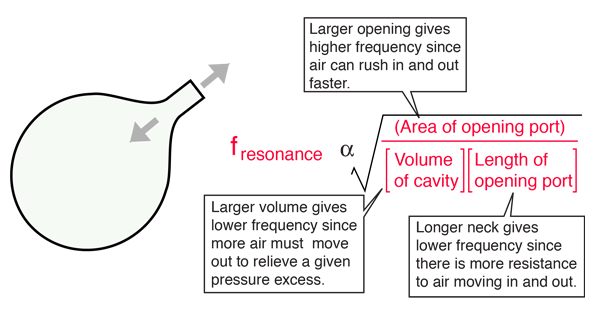
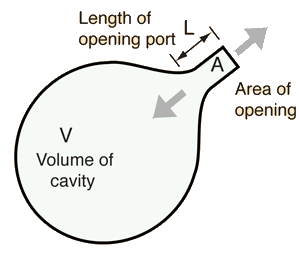
Thinking of the cavity resonance in terms of an oscillating mass of air can give some intuition about why the physical properties of the cavity affect the resonant frequency as they do. You can visualize the process of pushing extra air into the cavity to produce an overpressure. That overpressure represents stored energy in a way analogous to lifting a mass on a spring above its equilibrium position. If the opening to the cavity is larger, the excess air can escape more rapidly to bring the pressure down to atmospheric, and this leads to a higher cavity resonant frequency. If the neck of the cavity is longer, there is more resistance to the flow of the excess air and the resonant frequency is lowered. If the cavity volume is increased, then it takes a greater excess mass of air to produce a given overpressure, and it therefore takes longer for that excess pressure to be relieved. The larger cavity will have a lower resonant frequency.
|
Again visualizing the mass on a spring, we know that if we lift it from equilibrium and allow it to fall, it will not stop when it reaches that equilibrium point but will overshoot it and oscillate about equilibrium because the work we did to lift the mass put energy into the elastic system. Likewise, when we have done work to increase the pressure in a cavity, we have given it energy and as the air rushes out, it will overshoot the equilibrium (atmospheric pressure) and produce a slight vacuum in the cavity. This elastic system produces the cavity resonance, but it is highly damped and will not continue to oscillate like a mass on a spring.
|
Index
Wave concepts
Resonance concepts |