Photon-Electron Interaction
If a high energy photon interacts with an electron, the interaction can be described by the Compton scattering relationship or by the 4-vector formulation of relativistic momentum. As a specific example, consider a 10GeV photon in a head-on collision with an electron at rest.
If we apply the Compton formula
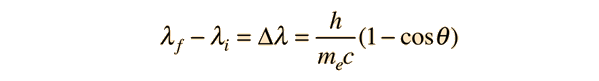
with λ = h/p (deBroglie relationship) for a back-scattered photon where θ = 180°, this relationship can be expressed
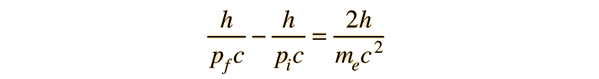
and rearranging gives

Since pic >> mec2
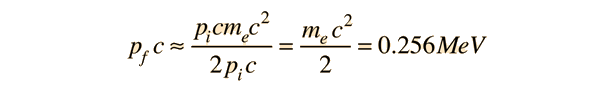
Conservation of energy then tells us that the electron energy after the collision is 9.999744 GeV. So essentially all of the energy of the photon is transferred to the electron. This situation can be pictured conceptually as follows:
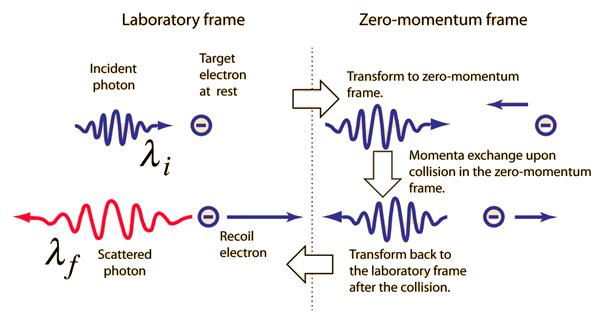
The conceptual description that leads you to the conclusion that the electron has most of the energy after the collision involves transforming the momenta to the zero-momentum frame, which diminishes the momentum of the photon while increasing that of the electron. Then the momenta exchange upon collision in the zero momentum frame. Then you make the reverse transformation which further reduces the magnitude of the photon momentum while increasing the momentum of the electron. For the extreme example used here, the electron gets most of the energy.
The transformation to the zero-momentum frame, however, is not a matter of transforming the photon down to 5 GeV and giving the electron a momentum -5GeV/c as you might expect. The transformation is much more drastic. It can be accomplished by using the energy and momentum as a 4-vector and doing the necessary Lorentz transformation.
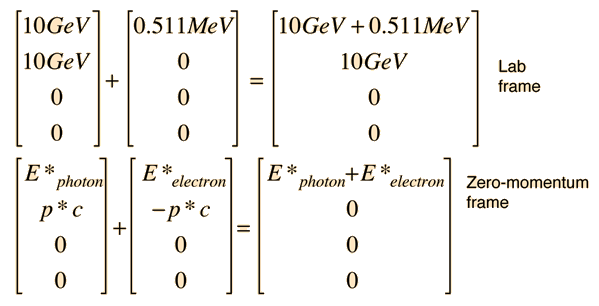
The tool to be used is the invariance of the length of the 4-vector upon transformation. Evaluated in the laboratory frame, it is
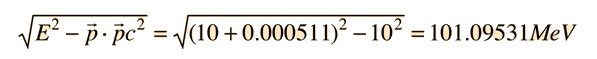
Then in the zero-momentum frame, this energy is divided between the photon and the electron in such a way that their momenta are equal in magnitude. Using the relativistic energy relationship to express the length of the 4-vector in terms of the momenta gives

Solving this equation iteratively gives p*c = 50.5476 MeV. Now we can determine the frame speed of the zero-momentum frame by determining the speed required to Doppler shift the 10 GeV photon down to 50.5476 MeV.
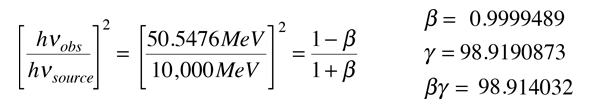
This allows us to set up the energy/momentum transformation.

This transformation does indeed give us zero momentum and conserve energy. Reversing the sign of β should take us back to the laboratory frame.

This transformation gives us the same results that were obtained by the Compton scattering approach.
| Lorentz transformation in 4-vector form |
| Four-vector sum for momentum-energy |
Reference
Rohlf
Sec 4-4
| HyperPhysics***** Relativity | R Nave |