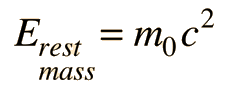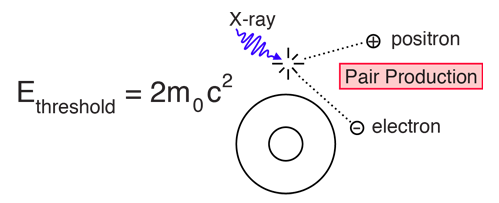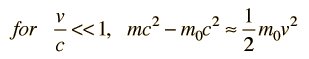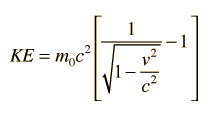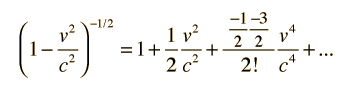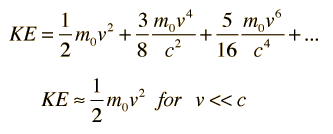Relativistic Energy
The famous Einstein relationship for energy

includes both the kinetic energy and rest mass energy for a particle. The kinetic energy of a high speed particle can be calculated from

The relativistic energy of a particle can also be expressed in terms of its momentum in the expression
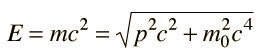 |
|
The relativistic energy expression is the tool used to calculate binding energies of nuclei and the energy yields of nuclear fission and fusion.
| HyperPhysics***** Relativity | R Nave |