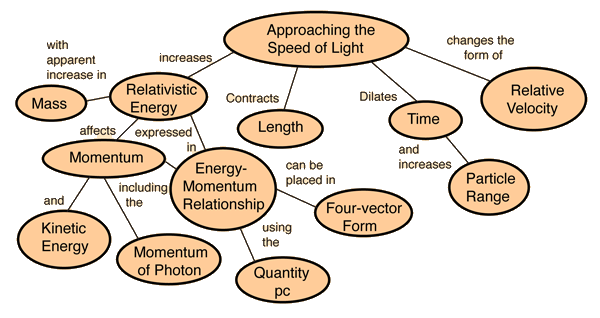
Relativistic Mechanical Quantities
A number of ordinary mechanical quantities take on a different form as the speed approaches the speed of light.
| At what energies must relativistic expressions be used? |
| HyperPhysics***** Relativity | R Nave |
Relativistic Mechanical QuantitiesA number of ordinary mechanical quantities take on a different form as the speed approaches the speed of light.

|
Index | ||
|
Go Back |
Relativistic MomentumThe relativistic momentum is given by 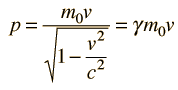 which is the ordinary definition of momentum with the mass replaced by the relativistic mass. In the above calculations, one of the ways of expressing mass and momentum is in terms of electron volts. It is typical in high energy physics, where relativistic quantities are encountered, to make use of the Einstein relationship to relate mass and momentum to energy. In relativistic mechanics, the quantity pc is often used in momentum discussions. It has the units of energy. 
A useful application of the quantity pc is in the calculation of the velocity as a fraction of c.
with the limiting case applying for the momentum of a photon.
|
Index | |||||||||
|
Go Back |
Momentum of Photon For a photon, the relativistic momentum expression 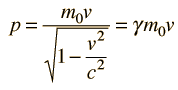 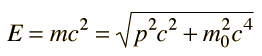 and by setting rest mass equal to zero and applying the Planck relationship, we get the momentum expression: 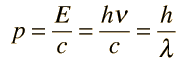
|
Index | ||
|
Go Back |
Relativistic Energy in Terms of MomentumThe famous Einstein relationship for energy 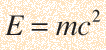 can be blended with the relativistic momentum expression 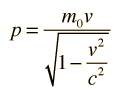 to give an alternative expression for energy. The combination pc shows up often in relativistic mechanics. It can be manipulated as follows: 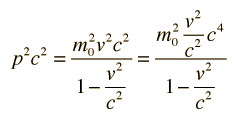 and by adding and subtracting a term it can be put in the form: 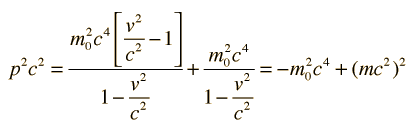 which may be rearranged to give the expression for energy: 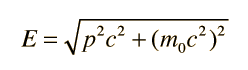 Note that the m with the zero subscript is the rest mass, and that m without a subscript is the effective relativistic mass. |
Index | ||
|
Go Back |