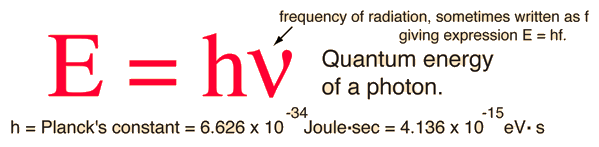Photons: The Quanta of Light
According to the Planck hypothesis, all electromagnetic radiation is quantized and occurs in finite "bundles" of energy which we call photons. The quantum of energy for a photon is not Planck's constant h itself, but the product of h and the frequency. The quantization implies that a photon of blue light of given frequency or wavelength will always have the same size quantum of energy. For example, a photon of blue light of wavelength 450 nm will always have 2.76 eV of energy. It occurs in quantized chunks of 2.76 eV, and you can't have half a photon of blue light - it always occurs in precisely the same sized energy chunks.
But the frequency available is continuous and has no upper or lower bound, so there is no finite lower limit or upper limit on the possible energy of a photon. On the upper side, there are practical limits because you have limited mechanisms for creating really high energy photons. Low energy photons abound, but when you get below radio frequencies, the photon energies are so tiny compared to room temperature thermal energy that you really never see them as distinct quantized entities - they are swamped in the background. Another way to say it is that in the low frequency limits, things just blend in with the classical treatment of things and a quantum treatment is not necessary.
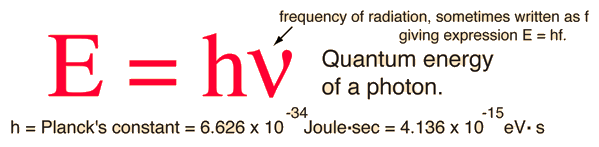
|
Index
Photoelectric effect |