Threshold for Relativistic Effects

At what energies is a particle relativistic? It is convenient to know ranges of energies at which non-relativistic approximations are good enough. The energies at which non-relativistic expressions for mechanical quantities of electrons and protons are in error by 1% is a reasonable threshold for relativistic treatments.

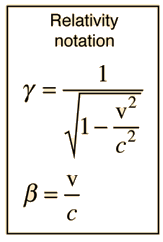
The relativistic momentum p = mv = γm0v departs by 1% from the non-relativistic expression when γ = 1.01 . This occurs for β = 0.14 or v = 0.14 c. The kinetic energy at this speed is (γ - 1)m0c2 = 0.01m0c2. The 1% threshold is then 5.11 keV for electrons and 9.38 MeV for protons. For alpha particles, the 1% threshold for momentum is at 37.27 MeV. Applied to radioactive decay energies of around 1-10 MeV, this suggests that essentially all beta decay electrons are relativistic, but no alpha particles are relativistic.

The relativistic kinetic energy

differs from the non-relativistic form of kinetic energy by 1% when

Solving this numerically gives γ = 1.00673 , so the 1% error threshold for electrons is 3.4 keV and that for protons is 6.3 MeV.

Taking another look at relativistic momentum, the exact expression for pc in terms of kinetic energy is

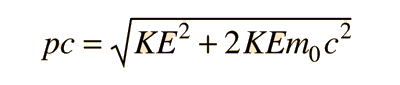
but for low energies, the square of the kinetic energy in this expression can be neglected, giving the simpler approximate expression

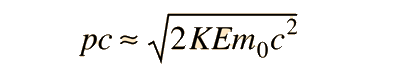
This simpler expression is accurate within 1% for electrons when KE < 20.7 keV and for protons when KE < 38 MeV.

Looking at the extreme relativistic case, the particle energy can be approximated by the photon energy expression E = hc/l = pc when the rest mass energy is negligible compared to the kinetic energy. This approximation is accurate within 1% when

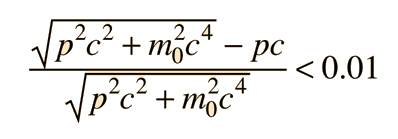
The approximation E=pc is accurate within less than 1% for electrons when pc > 3.6 MeV and for protons when pc > 6.6 GeV .