Relativistic Range

The ability to detect a short-lived particle depends upon it having enough range in the accelerator to reach the detector. This is a serious problem with particles which may have an average lifetime as short at 10-16 seconds! Even traveling at the speed of light, it will traveled only 0.03 micrometers before decaying, on average. The practical detection of short-lived particles depends upon relativistic time dilation.

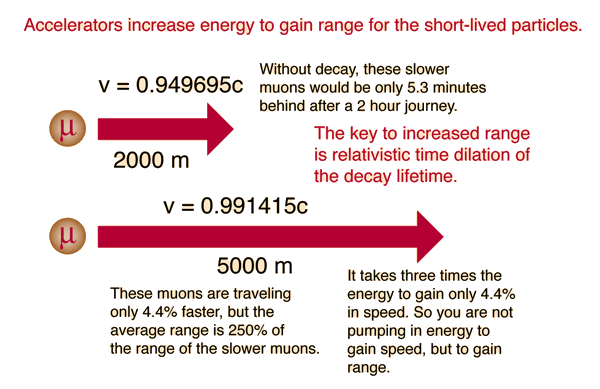
Because the clocks of the high speed particles run more slowly than the laboratory frame, the particles have a longer range in the accelerator than a non-relativistic treatment would anticipate. The numbers in the above illustration can be verified in the calculation below.

For a mass of
m =x10^kg = me = mp

with mass energy
m0c2 = x10^eV/c2 =MeV/c2 = GeV/c2

traveling at velocity
v = x10^ m/s = c, gamma = γ =

the kinetic energy is

K.E.(relativistic) =x10^ joules = x10^ eV.

If the mean lifetime of this particle is x10^s

then it's non-relativistic range would be x10^m.

With time dilation of the lifetime taken into account, the range would be
x10^m.

Note: Muon parameters will be entered by default. All values may be changed.

An example requiring the relativistic range to explain the observed data is the muon flux at the Earth's surface.

Relativistic Mechanical Quantities
An Overview of Time
 Index
 
HyperPhysics***** Relativity R Nave
 Go Back