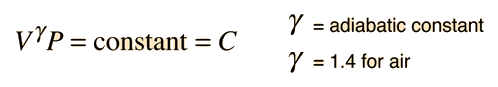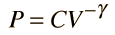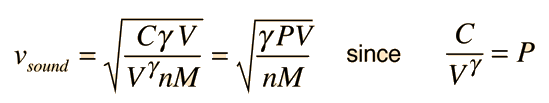Sound Speed in Gases
The speed of sound in an ideal gas is given by the relationship
 |
|
- R = the universal gas constant = 8.314 J/mol K,
- T = the absolute temperature
- M = the molecular weight of the gas in kg/mol
- γ = the adiabatic constant, characteristic of the specific gas
For air, the adiabatic constant γ = 1.4 and the average molecular mass for dry air is 28.95 gm/mol. This leads to
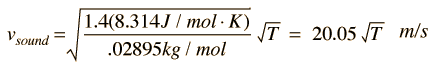
Doing this calculation for air at 0°C gives vsound = 331.39 m/s and at 1°C gives vsound = 332.00 m/s. This leads to a commonly used approximate formula for the sound speed in air:

For temperatures near room temperature, the speed of sound in air can be calculated from this convenient approximate relationship, but the more general relationship is needed for calculations in helium or other gases.
The calculation above was done for dry air, and moisture content in the air would be expected to increase the speed of sound slightly because the molecular weight of water vapor is 18 compared to 28.95 for dry air. A revised average molecular weight could be calculated based on the vapor pressure of water in the air. However, the assumption of an adiabatic constant of γ = 1.4 used in the calculation is based upon the diatomic molecules N2 and O2 and does not apply to water molecules. So the detailed modeling of the effect of water vapor on the speed of sound would have to settle on an appropriate value of γ to use.
| Table of sound speeds |
Traveling wave concepts
Sound propagation concepts
| HyperPhysics***** Sound | R Nave |