What is Temperature?
 The Zeroth Law of Thermodynamics | One approach to the definition of temperature is to consider three objects, say blocks of copper, iron and alumninum which are in contact such that they come to thermal equilibrium. By equilibrium we mean that they are no longer transferring any net energy to each other. We would then say that they are at the same temperature, and we would say that temperature is a property of these objects which implies that they will no longer transfer net energy to one another. We could say that A is at the same temperature as C even though they are not in contact with each other. This scenario is called the "zeroth law of thermodynamics" since this understanding logically precedes the ideas contained in the important First and Second Laws of Thermodynamics. |
 Kinetic temperature 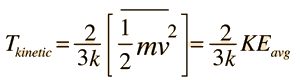 Ideas to think about:
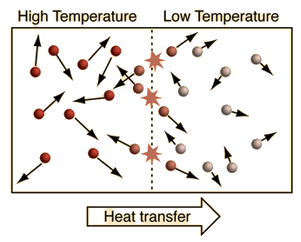
| An important idea related to temperature is the fact that a collision between a molecule with high kinetic energy and one with low kinetic energy will transfer energy to the molecule of lower kinetic energy. Part of the idea of temperature is that for two collections of the same type of molecules that are in contact with each other, the collection with higher average kinetic energy will transfer energy to the collection with lower average kinetic energy. We would say that the collection with higher kinetic energy has a higher temperature, and that net energy transfer will be from the higher temperature collection to the lower temperature collection, and not vice versa. Clearly, temperature has to do with the kinetic energy of the molecules, and if the molecules act like independent point masses, then we could define temperature in terms of the average translational kinetic energy of the molecules, the so-called "kinetic temperature". The average kinetic energy of the molecules of an object is an important part of the concept of temperature and provides some useful intuition about what temperature is. If all matter just consisted of independently moving point masses that just experienced elastic collisions with each other, that would be an adequate picture of temperature. |
Internal or coordinated motions of molecules complicate the picture of temperature. | Molecules for materials other than monoatomic noble gases like helium have the possibility of energy other than the translational kinetic energy of point masses. Molecules can have rotational and translational kinetic energy and the molecules in periodic solids can have collective modes of motion that have energy. This complicates the idea of temperature because they affect the conditions under which energy would be transferred from one collection of molecules to another, and we want to hang onto the idea that if energy is spontaneously transferred from A to B, then A is at a higher temperature than B. |
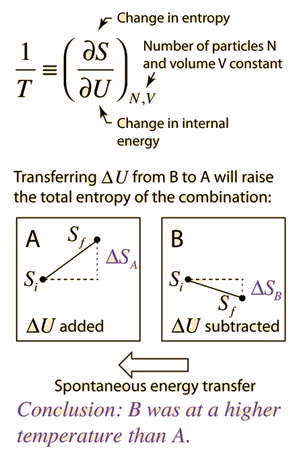
Defining temperature in terms of entropy. | Many of the most fundamental arguments in physics are those having to do with multiplicity. If there are more ways to accomplish a given state of a system of particles, then other states will spontaneously transition to that state over time if the transition is consistent with conservation of energy. The multiplicity of a system of particles is stated in terms of its entropy. Systems will spontaneously proceed toward states with higher entropy (2nd law of thermodynamics). But what does that have to do with temperature? It turns out that if you have two systems A and B which are thermally coupled to each other, and you make a change of internal energy ΔU to each of them, then if A experiences a larger change in entropy S than B, then A is the lower temperature and energy will spontaneously transfer from B to A. This is far less intuitive than high-speed molecules hitting low-speed molecules and transferring energy to them! But with the variety of energy forms and collective modes in systems, it turns out to be a more reliable approach to temperature. See the examples where this approach with the ideal gas and Einstein solid leads you back to the more intuitive kinetic energy statements. |
Under conditions where the kinetic temperature as derived from kinetic theory provides reasonable accuracy, we perceive temperature as the average translational kinetic energy associated with the disordered motion of atoms and molecules. That makes it intuitive that the flow of heat is from a high temperature region toward a lower temperature region since higher energy molecules are striking lower energy molecules and transferring energy to them. Temperature is not directly proportional to internal energy since temperature measures only the kinetic energy part of the internal energy, so two objects with the same temperature do not in general have the same internal energy (see water-metal example). Temperatures are measured in one of the three standard temperature scales (Celsius, Kelvin, and Fahrenheit).
| Suppose we are dealing with two equal mass objects at ordinary temperatures and can presume that kinetic temperature gives a reasonable description of their behavior. If the two objects are at the same temperature, then we would say that their average translational kinetic energies are the same. That does not imply that their total internal energies are the same, because the potential energies associated with intermolecular forces can be quite different. |
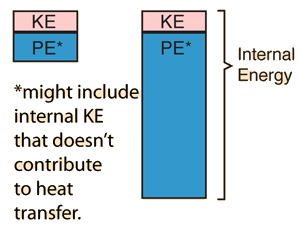 |
Even if there are internal kinetic energies other than translational KE, it could be that heat transfer is mainly by collisional transfer. In such cases this picture might help understand that just a portion of the total internal energy of objects is involved in the conditions for thermal equilibrium.
| Temperature Scales |
| More generalized view of temperature |
Temperature concepts
Reference:
Schroeder
Ch 3
| HyperPhysics***** Thermodynamics | R Nave |