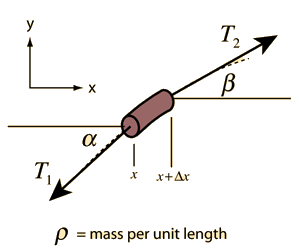
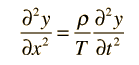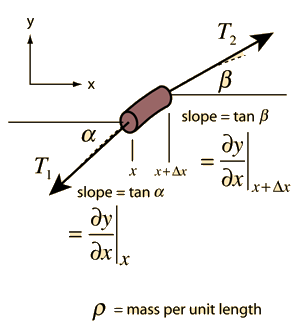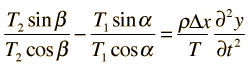The Wave Equation
The wave equation for a plane wave traveling in the x direction is
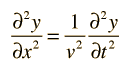
where v is the phase velocity of the wave and y represents the variable which is changing as the wave passes. This is the form of the wave equation which applies to a stretched string or a plane electromagnetic wave. The mathematical description of a wave makes use of partial derivatives.
In two dimensions, the wave equation takes the form
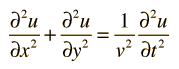
which could describe a wave on a stretched membrane.
| Varieties of wave equations |
Wave concepts
| HyperPhysics***** Sound | R Nave |