Time Dependent Acceleration
If a time dependent acceleration can be expressed as a polynomial in time, then the velocity and position can be obtained, provided the appropriate initial conditions are known. Allowing the acceleration to have terms up to the second power of time leads to the following motion equations for one dimensional motion.
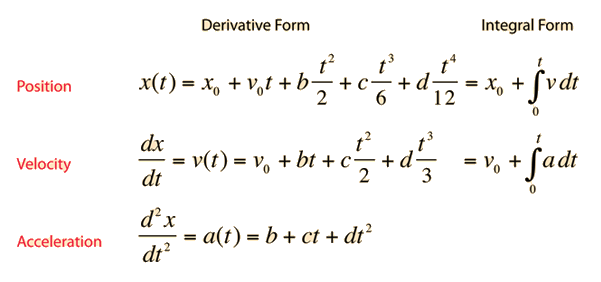
| Variable acceleration | Polynomial integrals | Polynomial derivatives | Calculation |
| Example problem |
Motion concepts
Velocity and acceleration
| HyperPhysics***** Mechanics | R Nave |