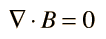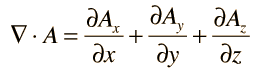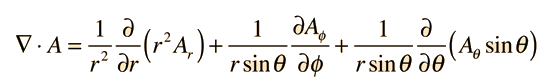The Divergence
The divergence of a vector field
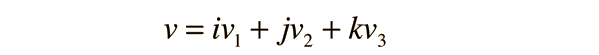
in rectangular coordinates is defined as the scalar product of the del operator and the function
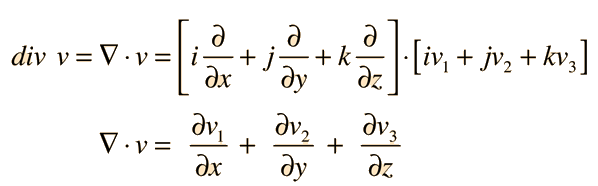
The divergence is a scalar function of a vector field. The divergence theorem is an important mathematical tool in electricity and magnetism.
Applications of divergence
Divergence in other coordinate systems
Vector calculus
| HyperPhysics*****HyperMath*****Calculus | R Nave |