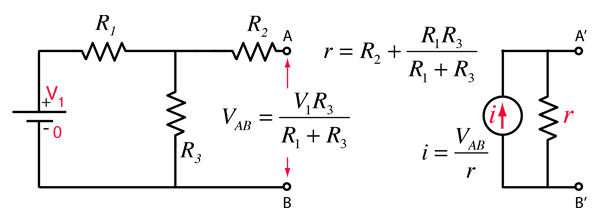
Norton's Theorem
Any collection of batteries and resistances with two terminals is electrically equivalent to an ideal current source i in parallel with a single resistor r. The value of r is the same as that in the Thevenin equivalent and the current i can be found by dividing the open circuit voltage by r.

| Norton current | Norton resistance | Numerical example | Thevenin equivalent |
DC Circuits
| HyperPhysics***** Electricity and Magnetism | R Nave |