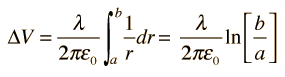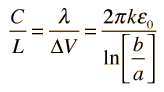
|
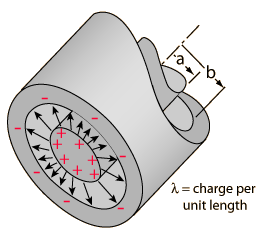
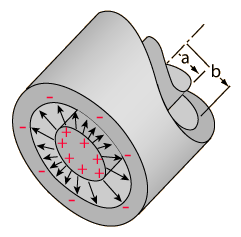
Cylindrical CapacitorFor a cylindrical geometry like a coaxial cable, the capacitance is usually stated as a capacitance per unit length. The charge resides on the outer surface of the inner conductor and the inner wall of the outer conductor. The capacitance expression is
|
Capacitor Concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |