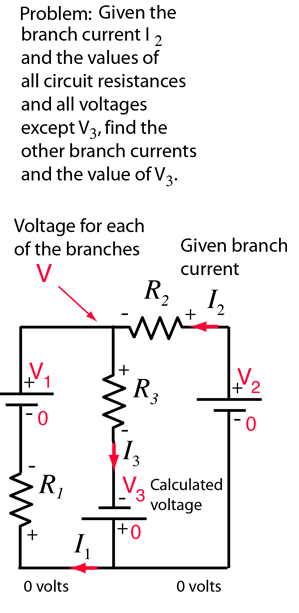
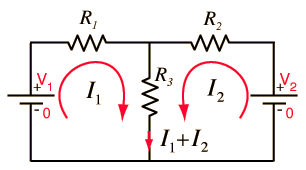
Two Loop Currents

Application of the voltage law and the current law. This approach requires two simultaneous equations formed by applying the voltage law to both loops. Taking the loops in the directions shown means that the sum of the currents flows through the middle resistor. Putting polarities on each component helps to keep the signs straight. The two loop equations are:

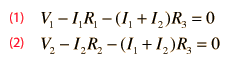Subtracting (2) from (1) and solving for the currents gives:

For R1 =Ω, R2 =

Ω, R3 =

Ω,

and voltages V1 = V and V2 = V,

the calculated currents are

= A,

= A.

Note: To avoid dealing with so many short circuits, any resistor with value zero will default to 1 when a voltage is changed. It can be changed back to a zero value if you wish to explore the effects of short circuits. Ohms and amperes are the default units, but if you put in resistor values in kilohms, then the currents will be milliamperes.

Strategy for a Two Loop Circuit

If you know one current in a two-loop circuit, say by measuring it with an ammeter, then the circuit can be simplified using the voltage law and the current law. This approach avoids the two simultaneous equations required for the general case.

Calculation for general two-loop, two-source circuit.

1. Note that the right hand branch must be analyzed first since it is the only one with full information. Find the voltage V at the top of the circuit. Note by the voltage law that V is the voltage for all three parallel branches. 2. The left branch mst be analyzed next since the center branch still has two unknowns. Find the branch current from 3. From the current law applied to the junction at top center Then find the unknown voltage from