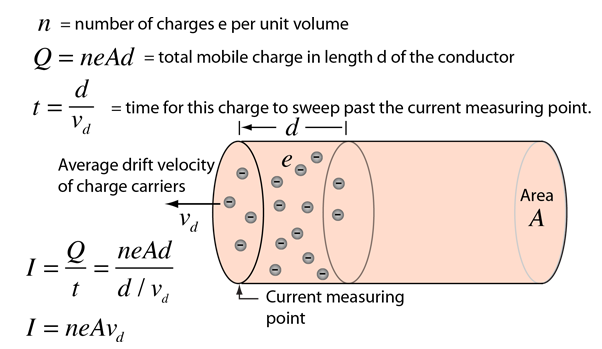
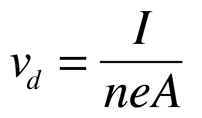Electric Charge Carriers
For electric current in a copper wire, the charge carriers are the mobile electrons and the positively charged copper ions are essentially stationary in the metal lattice. Nevertheless, treatments of electric circuits usually use conventional current, as if positive charges were moving. Debate continues about this practice, but the physical nature of the charge carriers in copper is fairly straightforward.
In other applications of electric current however, the identification of the charge carriers is not so simple. In semiconductors, for example, you sometimes have electrons which are mobile, and sometimes have deficiencies of electrons, called "holes" which are mobile. There are significant differences in the way they conduct. One way to detect which kind of conduction is taking place is with the Hall effect, which gives a different polarity for the Hall voltage for positive and negative charge carriers. In many substances, electric conduction is not just free electron movement.
|
Index
Electric current |