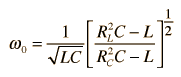Parallel Resonance
The resonance of a parallel RLC circuit is a bit more involved than the series resonance. The resonant frequency can be defined in three different ways, which converge on the same expression as the series resonant frequency if the resistance of the circuit is small.
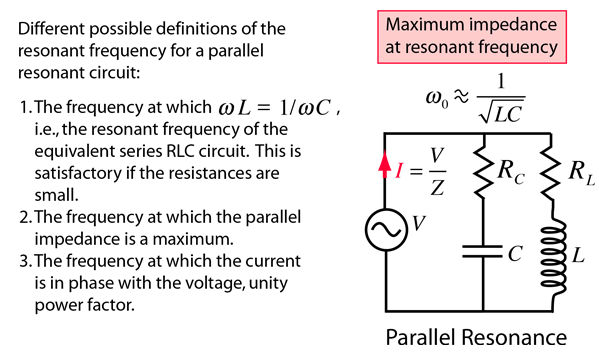
| Impedance definition | Phase definition |
AC Circuits
| HyperPhysics***** Electricity and Magnetism | R Nave |