Series-Parallel Combination
Most networks in AC circuits can be broken into blocks no more complicated than the one below. The complex impedance approach provides the tool necessary to reduce such a combination to an equivalent impedance. This kind of combination may be encountered in the development of an AC Thevenin equivalent for the analysis of an AC circuit.
 |
|
| The parallel part of the impedance can be put in the form | 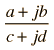 |
| which can be rationalized by the operation : | 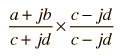 , , |
AC circuit concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |