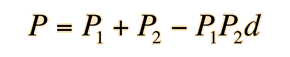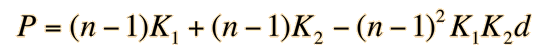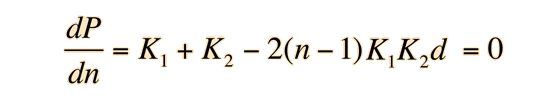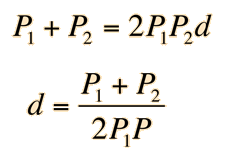Chromatic Aberration

A lens will not focus different colors in exactly the same place because the focal length depends on refraction and the index of refraction for blue light (short wavelengths) is larger than that of red light (long wavelengths). The amount of chromatic aberration depends on the dispersion of the glass.

One way to minimize this aberration is to use glasses of different dispersion in a doublet or other combination. Another approach uses spaced doublets.

Doublet for Chromatic Aberration

The use of a strong positive lens made from a low dispersion glass like crown glass coupled with a weaker high dispersion glass like flint glass can correct the chromatic aberration for two colors, e.g., red and blue.

Achromat Doublets

An achromat doublet does not completely eliminate chromatic aberration, but can eliminate it for two colors, say red and blue. The idea is to use a lens pair with the strongest lens of low dispersion coupled with a weaker one of high dispersion calculated to match the focal lengths for two chosen wavelengths. Cemented doublets of this type are a mainstay of lens design.

If the powers of the lenses of the doublet give a focus point in front of the doublet as shown above, it is said to be a positive achromat.

Chromatic aberration for three colors can be eliminated with and apochromat triplet.

Apochromatic Triplets

Better correction of chromatic aberration has been achieved than that afforded by the achromat doublets. One could use three lenses to achieve the same focal length for three wavelengths. In practice, so-called apochromatic lenses have been produced in the 4 to 16 mm focal length range for microscope objectives (Pedroti & Pedroti) with the use of fluorite elements.

Spaced Doublet Approach to Chromatic Aberration

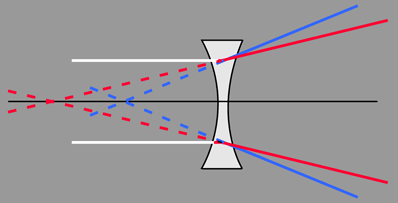
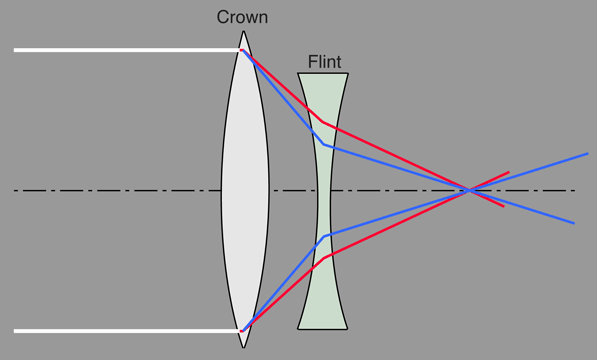
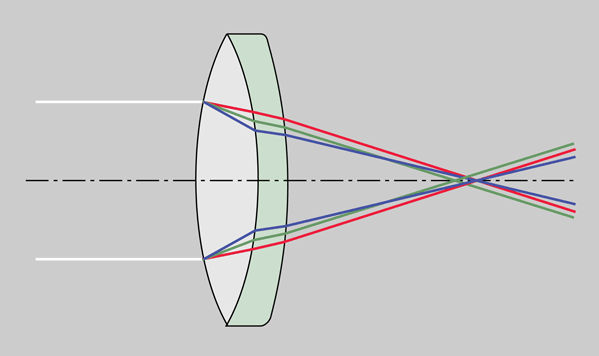
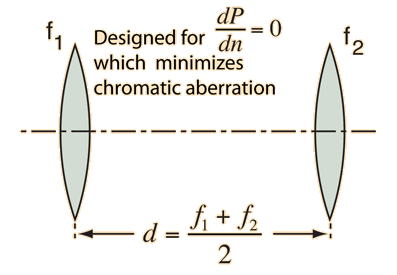Another approach to chromatic aberration reduction is to use two positive lenses separated by one half the sum of their wavelengths. Two equal positive lenses are used in eyepieces like the Ramsden eyepiece for correction.

This approach to minimizing chromatic aberration uses two lenses of the same type of glass so that there is just one index of refraction n, and the expression for the combined power of the lens combination depends upon that index of refraction. If you take the derivative of the power expression with respect to n and set it equal to zero, you can solve for the required separation of the lenses which makes that derivative equal to zero. The variation of index of refraction with light wavelength or color is called dispersion, and the zero derivative implies that the dispersion is zero. If the power does not depend on the index of refraction n, you have eliminated chromatic aberration. The caveat is that these expressions presume thin lenses and paraxial rays (close to optical axis), so it is not a perfect solution.

The power of a pair of thin lenses is given by

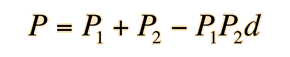
where the individual lens powers for a thin lens can be expressedd as

from the lens-makers formula. Here, K will be used to represent the dependence upon the radii of the lens surfaces. The power for the lens pair is then

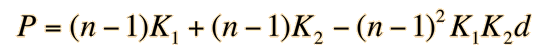
The derivative of the power with respect to n is

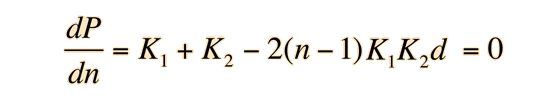
This is the condition for no change in lens power with respect to the index n, i.e., zero chromatic aberration. Multiplying by (n-1) allows us to express this in terms of the lens powers and yields

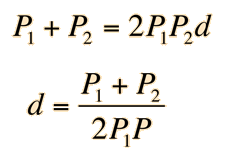
And using P=1/f this can be expressed in terms of the focal lengths

Note that if f₁ = f₂ the separation is just equal to the focal length of each of the lenses, and this condition is used for the Ramsden eypiece as mentioned above.