Lens-Maker's Formula
For a thin lens, the power is approximately the sum of the surface powers.
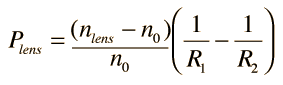
The radii of curvature here are measured according to the Cartesian sign convention. For a double convex lens the radius R1 is positive since it is measured from the front surface and extends right to the center of curvature. The radius R2 is negative since it extends left from the second surface.
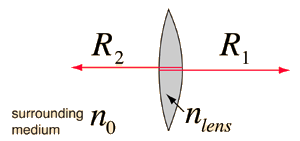
The above calculation is a single purpose calculation which returns the powers and focal lengths based on the values of the radii and indices of refraction. Substitute a number in any field and the calculation will be initiated. Default values will be entered for any unspecified parameter, but the index and radius values may be changed.
The second part of the calculation above shows the diminshed power of a lens in a medium other than air. This gives important insight into the role of the two lenses of the human eye. The cornea has the greatest power because light enters it from the air. The inner crystalline lens has much less refractive power because it is suspended in a water-like medium.
For thick lenses , Gullstrand's equation can be used to calculate the lens power.
Lens concepts
| HyperPhysics***** Light and Vision | R Nave |