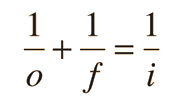Thin Lens Equation
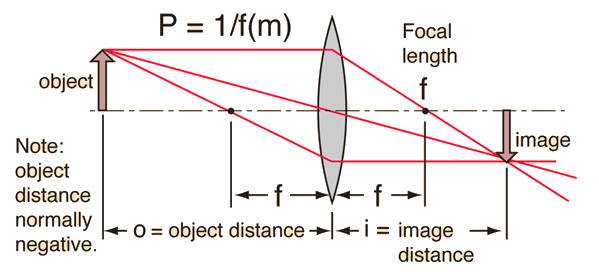
A common Gaussian form of the lens equation is shown below. This is the form used in most introductory textbooks. A form using the Cartesian sign convention is often used in more advanced texts because of advantages with multiple-lens systems and more complex optical instruments. Either form can be used with positive or negative lenses and predicts the formation of both real and virtual images. It is valid only for paraxial rays (rays close to the optic axis) and does not apply to thick lenses.

If the lens equation yields a negative image distance, then the image is a virtual image on the same side of the lens as the object. If it yields a negative focal length, then the lens is a diverging lens rather than the converging lens in the illustration. The lens equation can be used to calculate the image distance for either real or virtual images and for either positive on negative lenses. The linear magnification relationship allows you to predict the size of the image.
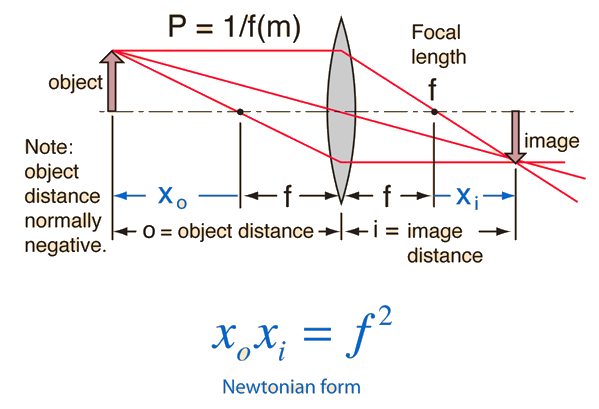
| Form of lens equation with Cartesian sign convention |
| Reversibility of object and image points: conjugate points |
Lens concepts
| HyperPhysics***** Light and Vision | R Nave |