Surface Power
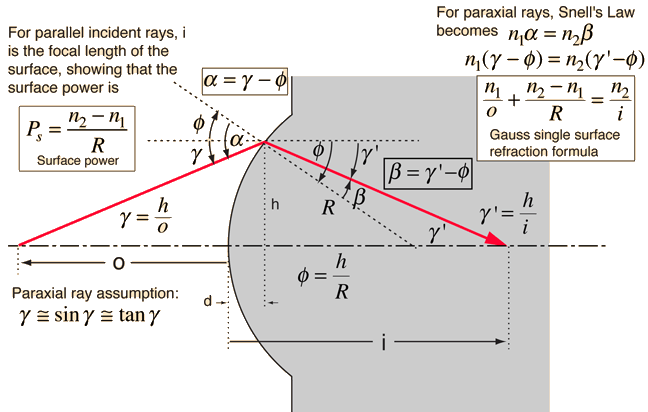
The surface power of a lens can be constructed geometrically as illustrated above. The relationships follow the sign convention used by Meyer-Arendt. It depends upon the indices of refraction and the radius of curvature of the surface. The power of a thin lens is approximately the sum of the surface powers of its surfaces. For a thicker lens, the surface powers can be used in Gullstrand's equation.
The expression for surface power obtained above is only valid for light rays at small angles where the angle in radians is approximately equal to the sine and the tangent of the angle. These rays are called paraxial rays. Most of the common expressions in geometrical optics are valid only in this paraxial approximation. Note that the distance d in the illustration above is left out of the expressions since for small angles it becomes very small.
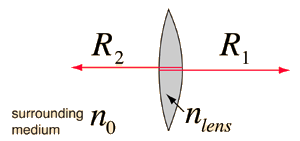 |
The surface power for a convex surface on the front vertex of a lens is positive because nlens>nair. If the back surface of a lens is convex, it also has a positive power since by the cartesian sign convention the radius is negative. For a thin lens, the power of the lens is approximately the sum of the surface powers. The relationship for lens power is called the lensmaker's formula. |
| Snell's Law |
Lens concepts
Thick lens concepts
Meyer-Arendt, 2nd Ed
Sec 1.3
| HyperPhysics***** Light and Vision | R Nave |