Principal Planes: Two Thin Lenses
The thin lens equation can be used with thick lenses or pairs of thin lenses if the principal planes are found.
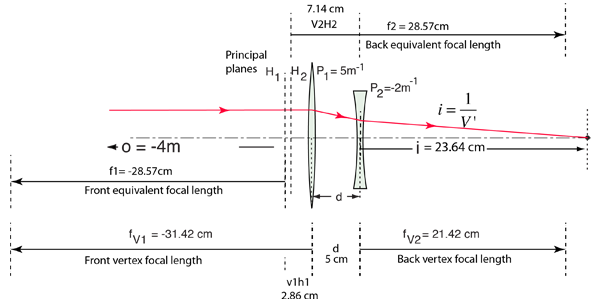
This is a sketch which attempts to give some perspective of the principal planes associated with two specific lenses. It is drawn to scale using results from the examination of the lenses using the system matrix approach. That approach allows you to calculate the locations of the two principal planes H1 and H2 and the relevant focal lengths which are associated with the lens system.
The locations and separation of the two principal planes depend upon the details of the lenses and their relative locations. This diagram just gives a specific example. The equivalent power of a pair of lenses can be calculated from Gullstrand's equation. Gullstrand's equation allows you to calculate the effective focal length f2 illustrated above with which you can approximately treat the two-lens system like a single lens with the lens equation. The error involved in such a treatment involves the separation between the principal planes H1 and H2, a distance that is basically left out in the treatment. The fact that the two principal planes shown are quite close together suggests that this system is a good candidate for such a treatment.
For this particular case, this principal plane treatment gives an image distance from the exit vertex of i = 23.64 cm. Using the simple lens equation with the equivalent focal length f2 = 28.57cm yields an image distance i = 30.77cm. But the equivalent focal length gives values with respect to principal plane H2 which is 7.14cm behind the exit vertex. When that is subtracted, the calculated image distance from the exit vertex is i = (30.77-7.14)cm = 23.63 cm.
| Principal planes | Single thick lens | Comparison to thin lens |
Lens concepts
Thick lens concepts
Reference
Meyer-Arendt
| HyperPhysics***** Light and Vision | R Nave |