The Astronomical Telescope

The diagram shows the standard astronomical telescope focused at infinity. This requires that the image formed by the objective be exactly at the focal length of the eyepiece. The astronomical telescope can be used to view objects at finite distances, although there is the inconvenience of having the image upside down. Nevertheless, showing the imaging details for finite distances is an interesting exercise in applying the lens equation. If used to view objects at a finite distance, the lens separation must be changed, as you can demonstrate by trying different distances in the calculation below.

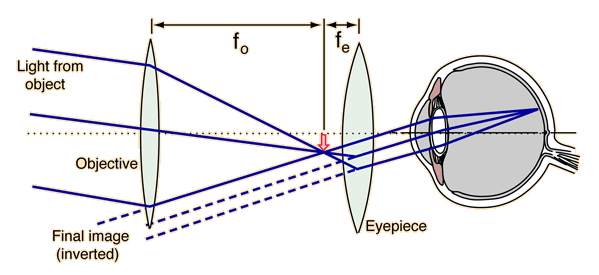
The above calculation assumes that the image is formed as a virtual image at infinity for comfortable viewing; this is the standard practice. The calculation involves application of the lens equation to calculate the image distance of th image formed by the objective lens in the tube of the telescope. Forcing the final image to be at infinity requires the real image formed by the objective to be at the focal length of the eyepiece.

If you insist, you can get more magnification from the telescope by adjusting the eyepiece to form its virtual image closer to the user's eye. If you bring it in to the standard close-focus distance of 25 cm, then applying the lens equation to both objective and eyepiece images shows that you must adjust the separation of the lenses to

You can get more magnification from the telescope by focusing it so that the virtual image is at 25 cm rather than infinity, but it is not a good idea because it puts the eye of the viewer under strain to accommodate the eye to that close distance. The relaxed eye is focused at infinity, so if you are going to use the telescope all day, you had better focus it at infinity.

The astronomical telescope can be used at different distances as shown be the above calculation, but if you insist on having your image right-side up, then you need to use a Galilean telescope, or use an inverting prism arrangement with the astronomical telescope.