Gravity Force of a Spherical Shell
A classic problem in mechanics is the calculation of the gravity force that would be experienced by a mass m that was attracted by a uniform spherical shell of mass M. The law of gravity applies, but calculus must be used to account for the fact that the mass is distributed over the surface of a sphere. The problem is envisioned as dividing an infinitesemally thin spherical shell of density σ per unit area into circular strips of infinitesemal width.
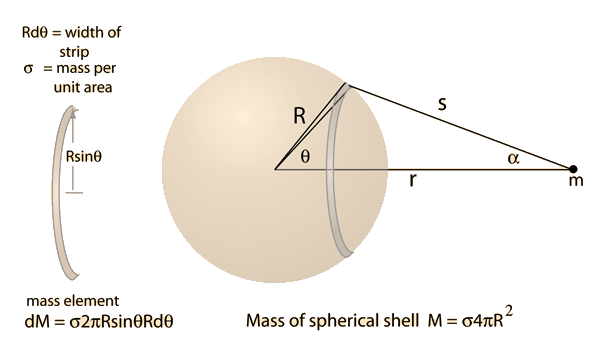
To set up the necessary integral, the triangle above is used to take advantage of the symmetry of the system. All components of the gravity force perpendicular to r will cancel by symmetry, and all components along r will sum. The differential element of force on mass m can be written

where the differential element of mass dM is given by
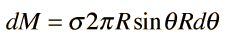
The force from the entire spherical shell can be expressed as an integral over the angle θ

To evaluate the integral, the variables s and α must be expressed in terms of the angle θ . Using the Law of Cosines with the interior angle θ gives

and this can be differentiated to give

Now using the Law of Cosines with the external angle α:
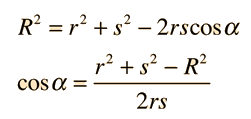
With these relationships, we can now express the integral in terms of s instead of θ, using the fact that s = r - R for θ = 0 and s = r + R for θ = π.
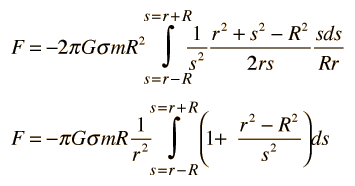
Using the area density expression σ = M/4πR2, the integral can be written
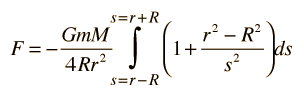
Now the parts are evaluated as polynomial integrals and simplified.
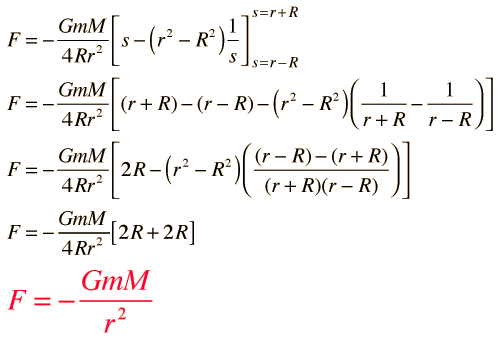
This is the desired goal, to show that the force from a thin spherical shell is exactly the same force as if the entire mass M were concentrated at the center of the sphere! Physically, this is a very important result because any spherically symmetric mass distribution can be build up as a series of such shells. This proves that the force from any spherically symmetric mass distribution on a mass outside its radius is the same as if the total mass were a point mass concentrated at the center of the sphere.
| Force on a mass inside a spherical shell |
Newton's laws
Gravity concepts
| HyperPhysics***** Mechanics | R Nave |