Powering a Laser
If a laser is continuously emitting light, then there must be power to replenish that lost energy in such a way that the laser action can continue. The power must maintain the necessary population inversion to keep the laser process going, and that implies a pumping mechanism to elevate electrons to that metastable state . The use of helium to "pump" electrons into a metastable state of neon in the helium-neon laser is an example of such a mechanism.
The minimum pumping power would occur if the pumping process were 100% efficient and you just had to replenish the energy lost in radiation. Lasers will have a finite bandwidth and a number of modes Nm within that bandwidth. The energy in a given mode can be charaterized by an average lifetime tc. Using the Planck relationship for the energy of a given photon, the minimum pumping power can be expressed by
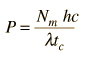
The rate of stimulated emission is proportional to the difference in the number of atoms in the excited state and the ground state, N2 - N1, which is in turn affected by the average lifetime of the excited state and the average lifetime of the emission in the laser cavity.
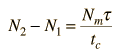 |
|
To obtain an estimate of the minimum pumping power, a cubical cavity of dimension L will be examined. A gas with an excited state of lifetime t is placed in the cavity. Doppler broadening will be presumed to set the linewidth and therefore the number of modes.
This calculation presumes that the laser condition above is met. This requires a proper combination of population inversion and lifetime of the excited state.
Laser concepts
Reference
Rohlf
Sec. 13-5
| HyperPhysics***** Quantum Physics ***** Optics | R Nave |