Total Internal Reflection
When light is incident upon a medium of lesser index of refraction, the ray is bent away from the normal, so the exit angle is greater than the incident angle. Such reflection is commonly called "internal reflection". The exit angle will then approach 90° for some critical incident angle θc, and for incident angles greater than the critical angle there will be total internal reflection.
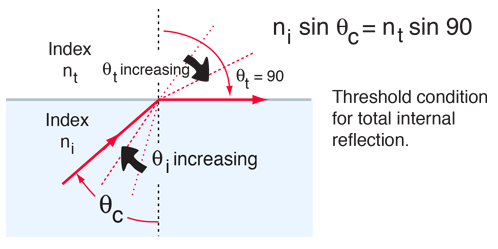
The critical angle can be calculated from Snell's law by setting the refraction angle equal to 90°. Total internal reflection is important in fiber optics and is employed in polarizing prisms.
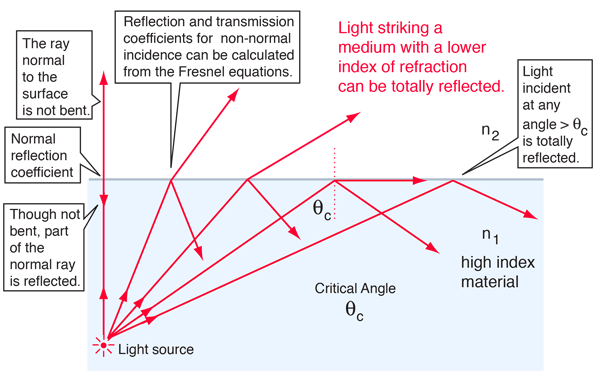
For any angle of incidence less than the critical angle, part of the incident light will be transmitted and part will be reflected. The normal incidence reflection coefficient can be calculated from the indices of refraction. For non-normal incidence, the transmission and reflection coefficients can be calculated from the Fresnel equations.
If values for n1 and n2 are entered above, the critical angle θc for total internal reflection will be calculated. (For example, θc = 48.6° for water and air.) But the angle for total internal reflection can be measured and used to determine the index of refraction of a medium. If a new value of θc is entered above, then the corresponding value of n1 will be calculated.
| Plot of internal reflection coefficients |
Reflection concepts
| HyperPhysics***** Light and Vision | R Nave |