Small vessels dominate resistance
Suppose you have a vessel that is 100cm long of diameter 5, but is then constricted to diameter 1 for just one centimeter of length. How much will that constriction increase the resistance to flow?
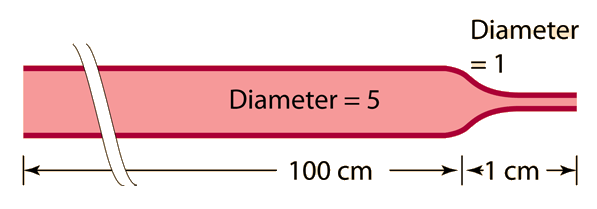
The large vessel has 100x the length, but the small vessel has 54 = 625 times the resistance per unit length. The 1 cm small section then has 6.25x the resistance of the entire length of larger vessel!
A small area of constriction in a blood vessel can make a large difference in the resistance to flow and can have major medical implications.
Resistances to fluid flow in a tube which are in series add directly, just like electrical resistances in series.
Poiseuille's law concepts
| HyperPhysics***** Mechanics ***** Fluids | R Nave |